線性回歸是利用最小平方法,對自變數與應變數擬合出一條回歸線的一種統計方法。只有一個自變數是簡單回歸,當自變數有多項時則稱為多元回歸。如何在兩個變數當中找出一條直線,讓這條直接最接近變數之間變動的斜率,是19世紀統計學的主題。簡單回歸的方程式透過下列關係式來描述:
\[y=\alpha x + \beta + \varepsilon, \varepsilon \sim N(0,\sigma^2)\]
也就是當\(x\)增加\(\alpha\)單位時,\(y\)會增加\(\alpha x+\beta\)。換句話說只要知道這條回歸線的斜率與常數項,就能從\(x\)來預測\(y\),而整個回歸分析的重點就在於找出\(\alpha\), \(\beta\)。其中
\[\alpha=\frac{n\displaystyle\sum_{j=1}^{n}{x_{j}}{y_{j}}-\displaystyle\sum_{j=1}^{n}{x_{j}}\displaystyle\sum_{j=1}^{n}{y_{j}}}{n\displaystyle\sum_{j=1}^{n}{x_{j}}^2-\left(\displaystyle\sum_{j=1}^{n}{x_{j}}\right)^2}, \beta=\frac{1}{n}\left(\displaystyle\sum_{j=1}^{n}y_{j}-\alpha\displaystyle\sum_{j=1}^{n}x_{j}\right)\]
最小平方法求回歸線的方法有很多種,除了上述公式外,可以參考LSM Step by Step。
簡單線性回歸
為了說明起見,我們以經濟學上著名的菲利浦曲線(Phillips Curve)來介紹回歸分析。這條曲線來自於紐西蘭籍經濟學家William Phillips在倫敦政經學院所發表的論文。在這篇名為The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861-1957的論文中,菲利浦從歷史數據中觀察到通貨膨脹與失業率的關聯,進而描繪出這條著名的曲線。
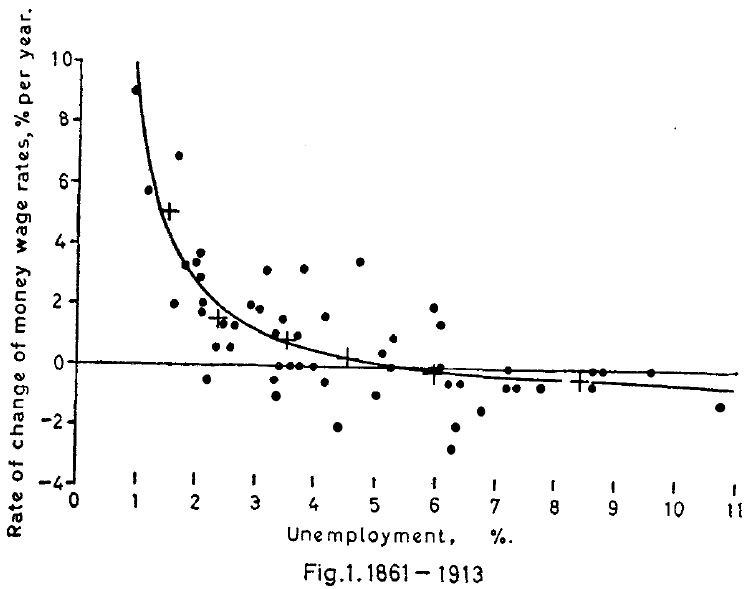
事實上我們可以看到,受限於早年資料取得的困難性,Phillips並不是直接以通貨膨脹率來分析,而是分析工資率漲跌與失業率之間的關係,因為在他的那篇經典論文中提到生活成本的調整會導致工資率的漲跌,進而影響勞動市場供需。我們仿照Phillips當年的作法,從中華民國統計資訊網彙整1990至2019年的工資變化率、失業率、物價指數成長率以及經濟成長率,來進行台灣版的菲利浦曲線。檔案已經存放在範例檔案中的phillips_curve.csv。
回歸模型
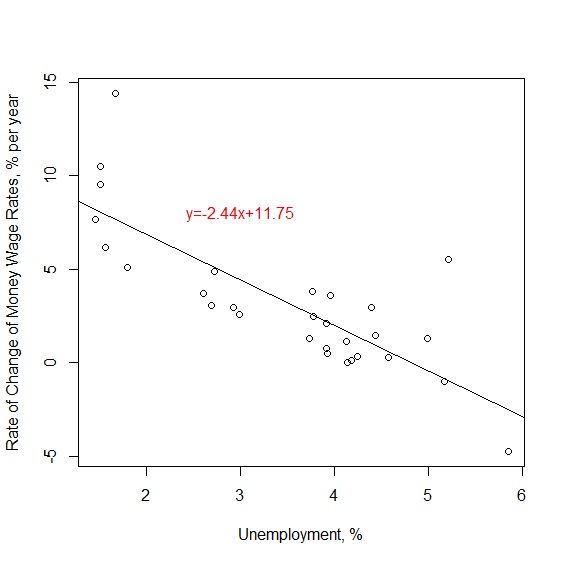
讀取資料後,用lm()指令,將wage當作應變數、unemployment當作自變數建構工資率與失業率的回歸模型。從分析結果可看到,台版菲利浦曲線回歸模型為\(y=-2.44x+11.75\)。
> phillips<-read.csv("c:/Users/USER/downloads/phillips_curve.csv", header=T, sep=",")
> names(phillips) #顯示變數名稱
[1] "year" "wage" "unemployment" "cpi"
[5] "growth"
> model<-lm(wage~unemployment, data=phillips) #建立工資率與失業率的回歸模型
> summary(model)
Call:
lm(formula = wage ~ unemployment, data = phillips)
Residuals:
Min 1Q Median 3Q Max
-2.2673 -1.6501 -0.5478 1.2494 6.7699
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.7449 1.3128 8.946 1.46e-09 ***
unemployment -2.4400 0.3533 -6.906 2.02e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.339 on 27 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.6385, Adjusted R-squared: 0.6252
F-statistic: 47.7 on 1 and 27 DF, p-value: 2.02e-07
一些相關的指令,可以呼叫回歸模型的詳細數據:
> confint(model, level=0.95) #信賴區間
> coefficients(model) #模型的係數與截距
> fitted(model) #依據模型所計算出來的y值
> residuals(model) #模型的殘差
接下來我們仿照Phillips當年的做法,畫一條台灣版的菲利浦曲線。從上述的模型可以發現這條回歸線的斜率為-2.44,斜率是負的代表工資變化率與失業率成反比:
> plot(x=phillips$unemployment, y=phillips$wage, xlab="Unemployment, %", ylab="Rate of Change of Money Wage Rates, % per year") #繪製散布圖
> abline(lm(phillips$wage~phillips$unemployment)) #在散布圖上加上回歸線
> text(x=3, y=8, col="red", "y=-2.44x+11.75") #在散布圖上加上回歸方程式
判定係數\(R^2\)
由於回歸模型是用最小平方法,擬合出一條回歸線,\(y\)能否被\(x\)完全解釋,取決於這條直線是不是能完全契合散布圖的形狀,也就是回歸模型的好壞。從散布圖中,我們可以知道回歸模型包含三種變異:總變異SST、可解釋變異SSR、其他變異SSE。聽起來有沒有一點熟悉?所以回歸模型的好壞,可以透過ANOVA來檢測。
> anova(model)
Analysis of Variance Table
Response: wage
Df Sum Sq Mean Sq F value Pr(>F)
unemployment 1 261.03 261.033 47.698 2.02e-07 ***
Residuals 27 147.76 5.473
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
既然已知總變異SST=可解釋變異SSR+其他變異SSE。那麼根據ANOVA就可計算模型的解釋力也就是判定係數\(R^2\)。
\(R^2=\frac{SSR}{SST}=\frac{261.03}{261.03+147.76}=0.6385\)
從判定係數可以得知,回歸模型大約可以解釋64%的變異量,同時ANOVA F檢定顯著,回歸模型中的個別變數t檢定失業率也顯著,代表這個台灣版的菲利浦曲線確實呈現失業率與工資變化率的關係。
模型診斷
和其他統計模型一樣,線性迴歸也有自己的前提條件,其中最重要的就是殘差必須符合常態分配,而且平方和具有一致性(homogeneity of the residual variance)。這是什麼意思呢?白話文就是,觀察值不能和擬合出來的回歸線距離太遠,否則殘差就越大,代表這條回歸線越不準確。事實上從ANOVA模型檢定與判定係數,已經可以大略知道殘差的情形,不過我們還是可以只針對殘差進行分析,有助於更加了解回歸模型。
下列是一些模型診斷常用的指令:
> residuals(model) #計算殘差
> influence(model) #輸出回歸模型診斷數據
圖形診斷
視覺診斷是最簡單判別殘差的方法,用plot()可以呼叫出4張殘差診斷圖。Residuals vs Fitted以及Scale-Location可以看出回歸模型與實際樣本的差異,Q-Q圖可以看出殘差是否符合常態分配,Residuals vs Leverage則可以透過「庫克距離」來衡量觀察值對模型的影響大小。
> layout(matrix(c(1,2,3,4),ncol=2, nrow=2, byrow=TRUE)) #設定2x2的layout來呈現4張殘差圖
> plot(model) #呼叫4張殘差診斷圖
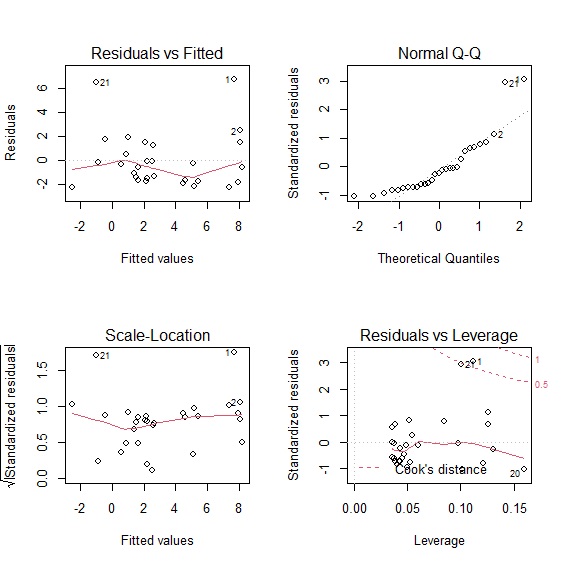
從4張殘差診斷圖中可以發現,台灣版菲利浦曲線的回歸模型,並沒有完全符合殘差常態分配的假定,殘差與樣本值的誤差也偏大,所以整體的模型解釋力只有0.6385。影響模型解釋力的主要因素,從4張診斷圖當中也可以發現那些樣本點是造成殘差的主要因素,也就是這些樣本屬於極端值。
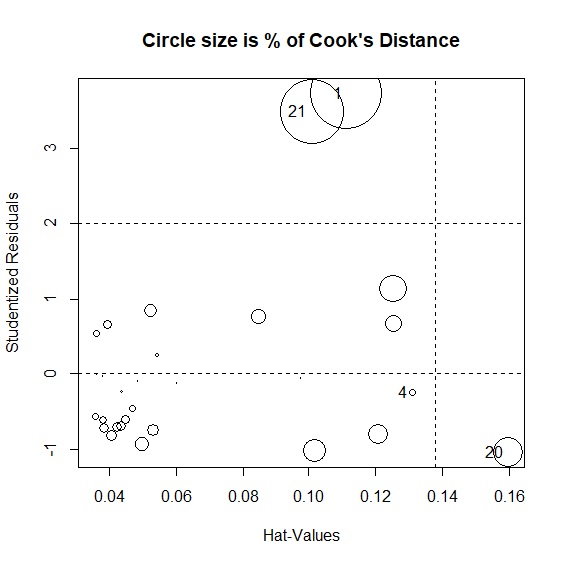
槓桿值與庫克距離
槓桿值與庫克距離是衡量離群值對模型影響的數值,可以透過influencePlot()繪圖來衡量,hatvalues()與cooks.distance()則可以實際計算每筆樣本的槓桿值與庫克距離。槓桿值與庫克距離的計算過程繁複,有興趣的人可以分別參閱槓桿值Step by Step以及庫克距離Step by Step,瞭解這兩個數值到底是怎麼計算出來的。
> library(car) #載入car套件
> layout(matrix(c(1), ncol=1, nrow=1)) #把圖形呈現的layout改回1x1
> influencePlot(model, main="Circle size is % of Cook's Distance") #繪製回歸模型診斷圖,並輸出離群值的槓桿值與庫克距離
StudRes Hat CookD
1 3.7339258 0.1114113 0.590828905
4 -0.2509052 0.1309457 0.004913307
20 -1.0468919 0.1597369 0.103806013
21 3.4950645 0.1006647 0.483014611
 > hatvalues(model) #計算每一個樣本的槓桿值
> hatvalues(model) #計算每一個樣本的槓桿值
> cooks.distance(model) #計算每一個樣本的庫克距離
殘差檢定
除了圖形診斷外,一些相關的統計量也提供了基本判斷標準,p值小於.05顯示不符合常態分配及殘差獨立性假設:
> shapiro.test(model$residual) #殘差常態分配檢定
Shapiro-Wilk normality test
data: model$residual
W = 0.80777, p-value = 0.0001155
> durbinWatsonTest(model) #殘差常態自我相關(獨立性)檢定
lag Autocorrelation D-W Statistic p-value
1 0.2252316 1.227507 0.04
Alternative hypothesis: rho != 0
> ncvTest(model) #變異數同質性檢定
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.3012812, Df = 1, p = 0.58308
多元線性回歸 / 複回歸
又稱為複回歸。與前面自變數都只有一個的情況不同,多元線性回歸具有兩個以上的自變數,線性回歸方程式加入另一個變數之後成為:\(y=\alpha x + \beta z + c\)。其實這已經不是一條直線,而是一個具有x、y、z軸的3D平面模型。我們現在將台灣版的菲利浦曲線,再加入一的自變數「經濟成長率」,來完成我們的多元回歸模型。
> MLR<-lm(wage~unemployment+growth, data=phillips)
> summary(MLR)
Call:
lm(formula = wage ~ unemployment + growth, data = phillips)
Residuals:
Min 1Q Median 3Q Max
-2.2662 -1.1801 -0.6977 1.2615 7.2979
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.2170 1.8964 4.333 0.000195 ***
unemployment -1.9822 0.3766 -5.264 1.68e-05 ***
growth 0.4035 0.1671 2.415 0.023076 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.155 on 26 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.7048, Adjusted R-squared: 0.6821
F-statistic: 31.03 on 2 and 26 DF, p-value: 1.295e-07
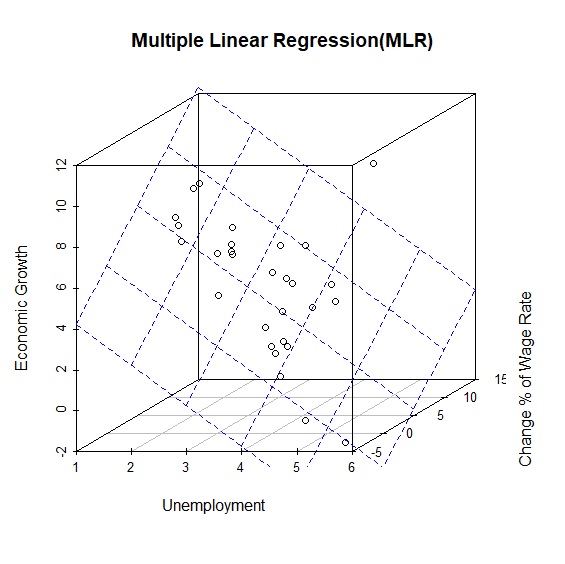
從上面分析顯示,多元回歸模型為\(y=-1.98x + 0.40z + 8.22\),判定係數\(R^2=0.7\)。由回歸係數可得知失業率與工資變化率呈反比,也就是菲利浦曲線的情況,而經濟成長率與工資變化率成正比,相當符合直覺。引進scatterplot3d()後,我們可以描繪3個變數的3D立體關係。
> library(scatterplot3d) #載入scatterplot3d套件
> s3d<-scatterplot3d(phillips$unemployment, phillips$wage, phillips$growth, #繪製立體3D散步圖,並將結果指定給s3d
+ xlab="Unemployment", ylab="Change % of Wage Rate", zlab="Economic Growth",
+ main="Multiple Linear Regression(MLR)")
s3d$plane3d(MLR, col="blue") #在s3d圖中繪製多元回歸模型平面
共線性
所有簡單線性回歸的模型診斷,包含殘差分析等,都適用多元回歸分析。這邊值得一提的是共線性(multicollinearity)問題,也就是兩個自變數是否高度相關。一般而言,當相關係數大於0.8時,代表變數關聯性強,這時只需要選擇其中一個納入回歸模型即可,否則會影響模型解釋力。
> cor(phillips, use="complete.obs") #排除遺漏值後進行相關分析
year wage unemployment cpi growth
year 1.0000000 -0.6252511 0.7062332 -0.5913482 -0.5159854
wage -0.6252511 1.0000000 -0.7990892 0.6952941 0.6246005
unemployment 0.7062332 -0.7990892 1.0000000 -0.7609087 -0.5033919
cpi -0.5913482 0.6952941 -0.7609087 1.0000000 0.4705541
growth -0.5159854 0.6246005 -0.5033919 0.4705541 1.0000000
相關分析顯示unemployment與growth的相關係數是-0.503。除此之外,變異數膨脹因子(Variance Inflation Factor, VIF)也是檢驗共線性的另一種方法。VIF應該越接近1越好,<5是可以接受的,但如果>10代表共線性的問題很大,不應該將變數納入模型,應該依據共線性大小逐一移除變數直到VIF<5為止。VIF的計算涉及輔助回歸,有興趣瞭解的人可以進一步參考VIF Step by Step。
我們的模型VIF=1.339,共線性問題不大。
> vif(MLR)
unemployment growth
1.339411 1.339411
交互作用
當兩個自變數不具備共線性(平行關係),同時又不互相獨立(正交關係)的時候,還是有可能對應變數\(Y\)存在局部的影響效果(斜交關係)。也就是兩個自變數藉由第三個變數來影響應變數的情況,這時候這第三個變數就稱為調節變數(moderator variable)。所以在模型上我們還可以加上一個調節變數,特別是在兩個自變數都沒有達到顯著的時候,有可能是透過調節變數來影響應變數。在模型上,可以用下列簡單的圖示表示:
數學式表達為:
\(y=\alpha+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{1}x_{2}+\epsilon\)
為什麼交互作用可以用\(x_{1}x_{2}\)來表示呢?其實只要把上述的式子移項,就可以得到一個以\(x_{1}\)斜率為主的方程式:
\(y=\alpha+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{1}x_{2}+\epsilon\)
\(=\alpha+\beta_{1}x_{1}+\beta_{3}x_{1}x_{2}+\beta_{2}x_{2}+\epsilon\)
\(=\alpha+(\beta_{1}+\beta_{3}x_{2})x_{1}+\beta_{2}x_{2}+\epsilon\)
\(=(\alpha+\beta_{2}x_{2})+(\beta_{1}+\beta_{3}x_{2})x_{1}+\epsilon\)
此時\(x_{1}\)的斜率為\(\beta_{1}+\beta_{3}x_{2}\),常數項是\(\alpha+\beta_{2}x_{2}\),\(\epsilon\)則是誤差項。以我們的模型為例,調節回歸必須先創造出一個相乘的新變數\(x_{3}\)。由此我們可以將失業率與經濟成長率相乘,嘗試一個調節回歸模型。
> MLR_mod<-lm(wage~unemployment+growth+unemployment*growth, data=phillips)
> summary(MLR_mod)
Call:
lm(formula = wage ~ unemployment + growth + I(unemployment *
growth), data = phillips)
Residuals:
Min 1Q Median 3Q Max
-2.2903 -1.1125 -0.4786 1.3615 7.0682
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.60412 4.40133 2.409 0.0237 **
unemployment -2.51309 0.95974 -2.619 0.0148 *
growth 0.03940 0.62732 0.063 0.9504
unemployment:growth 0.08066 0.13382 0.603 0.5521
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.181 on 25 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.709, Adjusted R-squared: 0.6741
F-statistic: 20.3 on 3 and 25 DF, p-value: 6.986e-07
根據上述結果,加入交互作用項\(x_{1}x_{2}\)的調節回歸方程式為:
\(y=10.60+0.04x_{2}+(-2.51+0.08x_{2})x_{1}\)
失業率\(x_{1}\)斜率為\((-2.51+0.08x_{2})x_{1}\),常數項則是\(10.60+0.04x_{2}\)。現在的重點是該如何詮釋這樣的結果?實務上,交互作用圖是一個相對簡單的方法,可以用肉眼看出\(x_{1}\)、\(x_{2}\)的關係,省去計算上的麻煩。這項工作可以透過interactions套件的probe_interaction()來達成。
> library(interactions)
> probe_interaction(MLR_mod, pred=unemployment, modx=growth, plot.points=TRUE, interval=TRUE)
JOHNSON-NEYMAN INTERVAL
When growth is INSIDE the interval [-3.00, 11.56], the slope of
unemployment is p < .05.
Note: The range of observed values of growth is [-1.61, 10.25]
SIMPLE SLOPES ANALYSIS
Slope of unemployment when growth = 1.944998 (- 1 SD):
Est. S.E. t val. p
------- ------ -------- ------
-2.36 0.73 -3.24 0.00
Slope of unemployment when growth = 4.765172 (Mean):
Est. S.E. t val. p
------- ------ -------- ------
-2.13 0.45 -4.71 0.00
Slope of unemployment when growth = 7.585347 (+ 1 SD):
Est. S.E. t val. p
------- ------ -------- ------
-1.90 0.40 -4.70 0.00
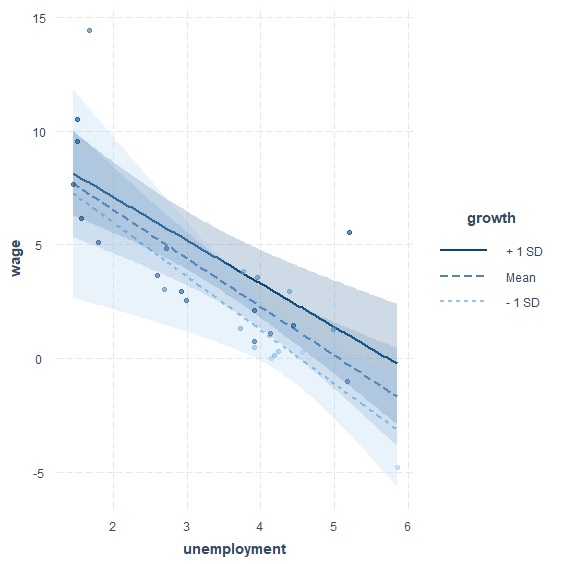
這張交互作用圖呈現在不同經濟成長率(growth)的情況下,失業率(unemployment)對工資變化率(wage)的影響。probe_interaction()分別計算了平均、大於一個標準差、小於一個標準差三種不同經濟成長率。從圖上來看—未達統計顯著所以不甚明顯—我們可以觀察到隨著經濟成長率越高,失業率的斜率有越來越平緩的趨勢。數據分析直接說明,當經濟成長率小於一個標準差的時候,斜率是-2.39,等於平均的時候斜率是-2.13,大於一個標準差的時候斜率是-1.90。
回到我們的問題,該如何解釋這樣的結果呢?菲利浦曲線證實失業率與通貨膨脹率的反向關係,而奧肯法則(Okun's Law)則證實失業率與經濟成長率的反向關係,所以其實這三個變數是互相影響的。也就是說,原本的多元回歸模型告訴我們失業率與經濟成長率都對工資成長率有影響,但納入調節變數之後可以觀察到,失業率的影響幅度,隨著經濟成長率越高,有越來越小的趨勢。我們可以不用標準化數據,直接用sim_slopes()搭配modxvals參數,指定經濟成長率的數字為0、5、10,會看得更明顯:
> sim_slopes(MLR_mod, pred=unemployment, modx=growth, modxvals=c(0,5,10))
JOHNSON-NEYMAN INTERVAL
When growth is INSIDE the interval [-3.00, 11.56], the slope of
unemployment is p < .05.
Note: The range of observed values of growth is [-1.61, 10.25]
SIMPLE SLOPES ANALYSIS
Slope of unemployment when growth = 0.00:
Est. S.E. t val. p
------- ------ -------- ------
-2.51 0.96 -2.62 0.01
Slope of unemployment when growth = 5.00:
Est. S.E. t val. p
------- ------ -------- ------
-2.11 0.44 -4.84 0.00
Slope of unemployment when growth = 10.00:
Est. S.E. t val. p
------- ------ -------- ------
-1.71 0.60 -2.87 0.01
當經濟成長率為0的時候,失業率的斜率是-2.51;成長率為10的時候,斜率降為-1.71。直接把數據帶入方程式的結果也是一致:
\(y=10.60+0.04x_{2}+(-2.51+0.08x_{2})x_{1}\)
當\(x_{2}=0\)時,斜率=\(-2.51+0.08 \times 0=-2.51\)
當\(x_{2}=5\)時,斜率=\(-2.51+0.08 \times 5=-2.11\)
當\(x_{2}=10\)時,斜率=\(-2.51+0.08 \times 10=-1.71\)
回歸模型納入調節變數後,因為是兩個自變數相乘,一個值得注意的問題就是共線性會變得異常大。這時候變數平均中心化(mean-centering)—把每個變數減去它的平均數—是一個避免共線性的常用技巧。jtools套件裡的center()提供一個平均中心化的功能。
> library(jtools) #載入jtools套件
> phillips_center<-center(phillips, binary.inputs="center") #將phillips的所有變數平均中心化
> MLR_mod2<-lm(wage~unemployment+growth+unemployment*growth, data=phillips_center) #用平均中心化的資料再跑一次回歸模型
> vif(MLR_mod) #平均中心化之前的模型共線性
unemployment growth unemployment:growth
8.48694 18.41673 14.10179
> vif(MLR_mod2) #平均中心化之後的模型共線性
unemployment growth unemployment:growth
1.883885 2.190252 1.710065
我們的調節回歸模型只有兩個自變數,萬一有三個自變數怎麼辦呢?此時兩兩交互作用有\(C_{2}^{3}\)種組合,再加上\(x_{1}x_{2}x_{3}\)全交互作用,回歸方程式會變成:
\(y=\alpha+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{3}+\beta_{4}x_{1}x_{2}+\beta_{5}x_{1}x_{3}+\beta_{6}x_{2}x_{3}+\beta_{7}x_{1}x_{2}x_{3}+\epsilon\)
如果要衡量\(x_{1}\)、\(x_{3}\)交互作用,只要令\(x_{2}=0\)就可得:
\(y=\alpha+\beta_{1}x_{1}+\beta_{3}x_{3}+\beta_{5}x_{1}x_{3}+\epsilon\)
如果要衡量\(x_{1}\)、\(x_{2}\)交互作用,只要令\(x_{3}=0\)就可得:
\(y=\alpha+\beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{4}x_{1}x_{2}+\epsilon\)
透過這個方法,還是可以一一衡量\(x_{1}x_{2}x_{3}\)交互作用的影響。

