R統計 | 無母數統計

統計分析經常需要確定樣本是否符合常態分配的假設，這是因為無論是平均數檢定、相關分析、變異數分析或回歸分析等方法都是建立在常態分配的假設上，這也是為什麼抽樣需要有足夠樣本，因為根據中央極限定理，當樣本數夠大的時候分布會趨近常態分配的鐘型曲線。那麼我們要問的是：「萬一樣本數不夠大的時候呢？」

當樣本數太小不足以形成常態分配，或樣本根本不是常態分配的時候，就沒有辦法用母體分配的參數，例如平均數、變異數來進行統計推論，這時候就需要運用到無母數的方法。無母數統計通常不需要事先知道母體分配長什麼樣子，所以也稱為「自由分配法」(distribution-free method)，是小樣本分析最常見的統計方法。

樣本到底是不是常態分配？

母數統計還是無母數統計取決於樣本是不是常態分配。要檢驗樣本是不是符合這項假定，直接用肉眼觀察直方圖或Q-Q圖是最簡單有效的方法。萬一不符合常態分配，通常還有下列補救方法：

樣本取對數
樣本開根號
無母數統計

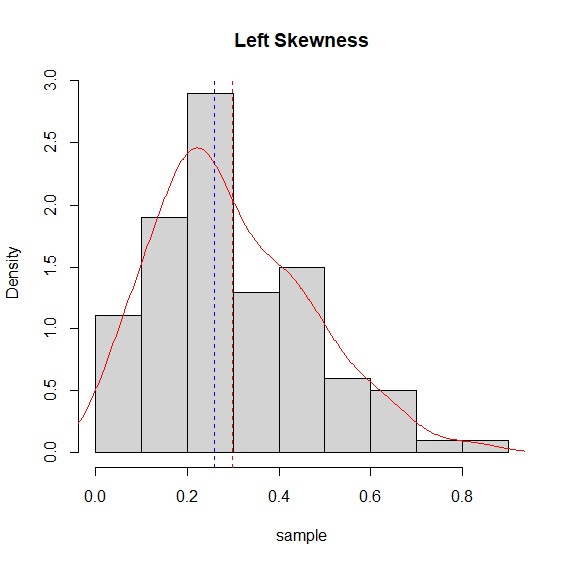
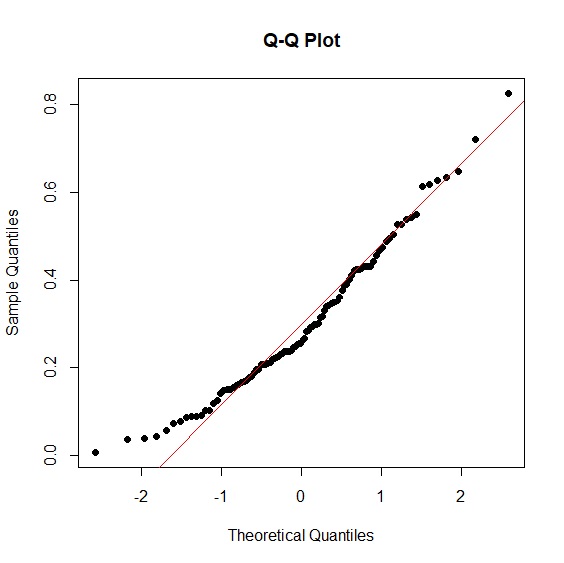
先來介紹對數與開根號的方法。beta分配很容易創造出偏態分配，所以我們以beta分配來驗證這兩種補救方法，也一併說明常態分配檢定的方法。首先以rbeta()指令創造出一個包含100個樣本的資料。直方圖一眼就能明瞭這是一個左偏分配。Q-Q圖的資料點偏離紅色直線，也說明這不是一個常態分配。


     > sample<-rbeta(n=100, shape1=2, shape2=5)
     
     > hist(sample, main="Left Skewness", freq=FALSE)

     > lines(density(sample), col="red")

     > abline(v=c(mean(sample), median(sample)), col=c("red", "blue"), lty=c(2,2))

     > qqnorm(sample, main="Q-Q Plot", pch=16)

     > qqline(sample, col="red")

萬一肉眼還是無法判斷或覺得一定要檢定才比較保險，shapiro.test()可以完成這項工作。shapiro檢定p值<.05表示資料與常態分配有顯著差異，>.05代表資料與常態分配一致。我們的例子p值<.05不符合常態分配，與肉眼觀察的結論一致。


     > shapiro.test(sample)

     

             Shapiro-Wilk normality test
     

     data:  sample
     W = 0.96423, p-value = 0.008141

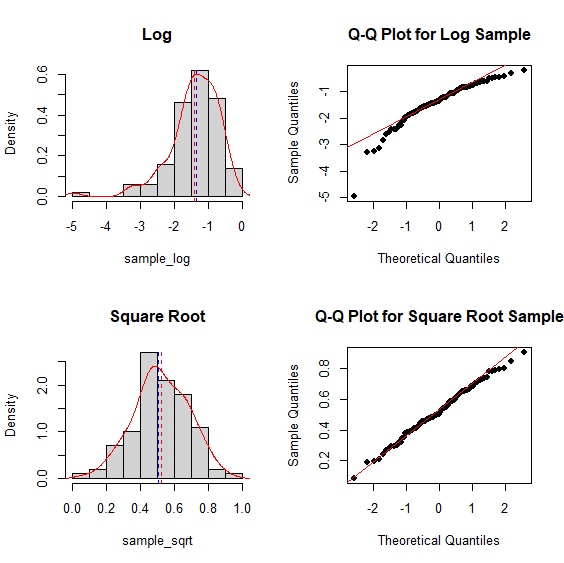
我們現在試著以對數與開根號來補救。實際操作後取對數後，分配從左偏變成右偏，但開根號後就已近似常態分配。


     > par(mfrow=c(2,2))

     > hist(sample_log, main="Log", freq=FALSE)

     > lines(density(sample_log), col="red")

     > abline(v=c(mean(sample_sqrt), median(sample_sqrt)), col=c("red", "blue"), lty=c(2,2))

     > qqnorm(sample_log, main="Q-Q Plot for Log Sample", pch=16)

     > qqline(sample_log, col="red")

     > hist(sample_sqrt, main="Square Root", freq=FALSE)

     > lines(density(sample_sqrt), col="red")

     > abline(v=c(mean(sample_log), median(sample_log)), col=c("red", "blue"), lty=c(2,2))

     > qqnorm(sample_sqrt, main="Q-Q Plot for Square Root Sample", pch=16)

     > qqline(sample_sqrt, col="red")

shapiro檢定p值>.05，證實樣本經過開根號後與常態分配一致。


     > shapiro.test(sample_sqrt)

     

             Shapiro-Wilk normality test
     

     data:  sample_sqrt
     W = 0.99498, p-value = 0.9747

萬一取對數、開根號都沒有辦法符合常態分配的要求怎麼辦？最終還有無母數統計可以用。下表列出一般常用統計方法及其對應的無母數統計法：

常用統計	須符合常態分配	無母數統計
獨立樣本t檢定	應變數	Mann-Whitney U test
成對樣本t檢定	成對樣本差	Wilcoxon signed rank test
單因子變異數分析	應變數與殘差	Kruskal-Wallis test
相關係數	兩個待驗變數	Spearman's \(\rho\), Kendall's \(\tau\)

曼-惠特尼U檢定 Mann-Whitney U Test

也稱做Mann-Whitney-Wilcoxon(MWW)檢定。這個由Ohio State University數理統計系教授Henry Mann與他的學生Donald Whitney在1947年發表統計方法。曼-惠特尼U檢定與魏克生等級和檢定(Wilcoxon Rank Sum Test)其實是類似的方法，都是用來檢定兩個獨立樣本中位數是否有差異，適用於不知道母體分配或不是常態分配的情況，特別適用於順序尺度的資料。兩種檢定所獲得的結論相同，因此R的指令無論是U檢定或是等級和檢定都是wilcox.test(paired=FALSE)。曼-惠特尼U檢定其統計量公式為：

\[U=min(U_{1},U_{2})\]

\[U_{1}=n_{1}n_{2}+\frac{n_{1}(n_{1}+1)}{2}-R_{1}, \text{where } R_{1}= \text{變數1的等級總和}\]

\[U_{2}=n_{1}n_{2}+\frac{n_{2}(n_{2}+1)}{2}-R_{2}, \text{where } R_{2}= \text{變數2的等級總和}\]

我們以美麗島電子報發布的2021年國政民調來說明曼-惠特尼U檢定的應用。formosa_survey.csv已經整理2021年1月到12月的總統執政滿意度、行政院長施政滿意度、執政黨好感度、最大在野黨好感度。我們想知道的是閣揆施政滿意度與執政黨好感度是否有差異？因為是小樣本所以執行曼-惠特尼U檢定。檢定結果p值>.05，因此閣揆的施政滿意度與執政黨好感度沒有顯著差異。關於曼-惠特尼U檢定的手動計算，有興趣的人可以參考M-W U Test Step by Step。


     > FormosaSurvey<-read.csv("c:/Users/USER/Downloads/formosa_survey.csv", header=T, sep=",")

     > FormosaSurvey

        president prime.minister   dpp   kmt
     1      0.578          0.520 0.504 0.336
     2      0.598          0.542 0.531 0.333
     3      0.593          0.535 0.508 0.354
     ⋮
     11     0.555          0.482 0.489 0.278
     12     0.546          0.483 0.461 0.280
     > wilcox.test(FormosaSurvey$dpp, FormosaSurvey$prime.minister, paired=FALSE)

     

             Wilcoxon rank sum exact test
     

     data:  FormosaSurvey$dpp and FormosaSurvey$prime.minister
     W = 52, p-value = 0.2657
     alternative hypothesis: true location shift is not equal to 0

魏克生等級和檢定 Wilcoxon Rank Sum Test

Frank Wilcoxon在1945年的論文提出等級和檢定(Wilcoxon Rank Sum Test)以及符號等級檢定(Wilcoxon Signed Rank Test)，讓這兩個方法迄今仍以他的名字來命名。等級和檢定其實就是U檢定中的R，R的指令一樣是wilcox.test(paired=FALSE)。

我們同樣以美麗島電子報發布的2021年國政民調來說明魏克生等級和檢定的應用。這次我們比較執政黨與最大在野黨的民眾好感度是否有差異？魏克生等級和檢定結果p值<.05，顯示兩個政黨在民眾的心中有明顯差異。有興趣瞭解手動計算可以參考Wilcoxon Rank Step by Step。


     > wilcox.test(FormosaSurvey$dpp, FormosaSurvey$prime.minister, paired=FALSE)

     

             Wilcoxon rank sum test with continuity correction
     

     data:  FormosaSurvey$dpp and FormosaSurvey$kmt
     W = 144, p-value = 3.63e-05
     alternative hypothesis: true location shift is not equal to 0

魏克生符號等級檢定 Wilcoxon Signed Rank Test

符號檢定是檢定單一樣本與特定中位數的差異，或兩組成對樣本有無差異的方法，可以看做是另類的成對樣本t檢定。它最初個概念只是比較樣本與中位數的大小，大於中位數的樣本取+，小於中位數的樣本取−，然後計算全部+的個數。因為只有正負兩種型態所以會服從二項分布，大於+的機率為50%。有鑒於符號檢定只有正負沒有差距的概念，魏克生納入每個樣本距離中位數的大小等級，將本來只有正負的符號改為有等級的概念，讓檢定力更為提升。其統計量為：

\[R=min(R^+, R^-)\]

covid-19疫情影響最大的莫過於航空及旅遊業，在邊境管制與隔離的情況下，全球航班大減。台灣儘管疫情相對緩和，但受到其他國家邊境封鎖的情況下，以往出國的熱潮以不復見。departure.csv整理了2019年到2020年桃園機場客運量。我們以魏克生符號等級檢定比較疫情爆發前後離境出國人數的差異。檢定結果p值不僅<.05還<.001顯示疫情的巨大衝擊。其手動計算可以參考Wilcoxon Sign Step by Step。


     > departure<-read.csv("c:/Users/USER/Downloads/departure.csv", header=T, sep=",")

     > departure

        year departure
     1  2019   2057706
     2  2019   1930695
     3  2019   2056959
     ⋮
     23 2020     40666
     24 2020     39025
     > wilcox.test(departure~year, paired=TRUE, data=departure)

     

             Wilcoxon signed rank exact test
     

     data:  departure by year
     V = 77, p-value = 0.0009766
     alternative hypothesis: true location shift is not equal to 0

克拉斯卡－瓦立斯檢定 Kruskal-Wallis Test

變異數分析假定母體為常態分配且變異數相等，當假定不能成立或資料為順序資料，變異數分析就不適用，這時候就能利用克拉斯卡－瓦立斯檢定(Kruskal-Wallis Test)完成3個以上群體的中位數檢定。其統計量為：

\[K=(N-1)\frac{\sum_{i=1}^g n_{i} (\bar{r_{i}}-\bar{R})^2}{\sum_{i=1}^g \sum_{j=1}^{n_{i}}(r_{ij}-\bar{R})^2}\]

雖然公式複雜，其實克拉斯卡－瓦立斯檢定是U檢定的延伸，一樣是將每個樣本給與順序等級，再將所有等級加總得到每個組別的\(r_{i}\)以及全樣本的等級和\(R\)。

烏魚是一種季節性洄游魚類，對海水溫度和鹽度敏感，需有適當溫度與鹽度的海域才能產卵，所以每年冬天會有一大群烏魚隨著親潮從北方向南洄游來到台灣附近海域過冬，其烏魚子更是深受喜愛的美食。除了近海、沿岸捕獲的野生烏魚外，近年受到氣候變遷、海洋暖化等因素影響野生烏魚產量衰退，市場主流逐漸被養殖烏魚所取代，從新竹以南到高屏都有烏魚養殖場，是西部沿海重要產業。

近年烏魚漁獲量取自漁業署的漁業統計年報，整理成mullet.csv。這個資料檔收錄了2011至2020共十年的台灣烏魚漁獲量以公噸表示，並依捕獲區域分為近海、沿岸、養殖三種。我們藉此以克拉斯卡－瓦立斯檢定來比較三種魚獲區域的產量是否有所不同。結果顯示p值<.05，近海、沿岸、養殖三種區域所捕獲的漁獲量有顯著差異。關於克拉斯卡—瓦立斯檢定的手動計算可以參考K-W Step by Step。


      > mullet<-read.csv("c:/Users/USER/Downloads/mullet.csv", header=T, sep=",")

      > mullet

         year     fishery mullet
      1  2011    offshore    221
      2  2012    offshore    756
      3  2013    offshore    514
      ⋮
      29 2019 aquaculture   1985
      30 2020 aquaculture   1326
      > kruskal.test(mullet~fishery, data=mullet)

      

              Kruskal-Wallis rank sum test
      

      data:  mullet by fishery
      Kruskal-Wallis chi-squared = 22.764, df = 2, p-value = 1.14e-05

斯皮爾曼與肯道爾等級相關係數 Spearman's \(\rho\) & Kendall's \(\tau\)

Charles Spearman(1904)賦予相關係數「等級」的概念，迄今仍是衡量兩個變數相關性的無母數指標。一個有趣的插曲是這篇論文第77頁，Spearman引用皮爾森相關係數公式時，犯了一個把平均數當作中位數的明顯錯誤，不過這個小瑕疵一點都不影響這篇論文的重要性。斯皮爾曼等級相關係數的公式與皮爾森相關係數相同，只不過把本來的數值換成等級來計算。在兩個變數等級都不相同的情況下，實際應用中它有個更方便的公式：

\[\rho=1-\frac{6 \sum d_{i}^2}{n(n^2-1)}\]

另一個等級相關係數是以同樣來自英國的Maurice Kendall為名的\(\tau\)。\(\tau\)雖然實際很少應用，但實際上在面臨樣本數很小且有很多等級相同的情況，\(\tau\)會比\(\rho\)來得好。Kendall's \(\tau\)根據不同數據情況衍生出三種計算方式，計算出來通常會小於\(\rho\)，其最基本的公式為：

\[\tau=\frac{協調配對的個數數目-不協調配對的個數數目}{\binom{n}{2}}\]

這裡同樣以美麗島電子報的2021年國政民調比較總統與閣揆施政滿意度在皮爾森、斯皮爾曼、肯道爾三種相關係數下的關聯性。三種相關係數在R都是用cor.test()藉由設定不同的method參數來完成。

Pearson's \(r\)


      FormosaSurvey<-read.csv("c:/Users/USER/Downloads/formosa_survey.csv", header=T, sep=",")

      > attach(FormosaSurvey)

      > cor.test(president, prime.minister, method=c("pearson"))

      

              Pearson's product-moment correlation
      

      data:  president and prime.minister
      t = 9.5892, df = 10, p-value = 2.332e-06
      alternative hypothesis: true correlation is not equal to 0
      95 percent confidence interval:
       0.8259683 0.9861258
      sample estimates:
            cor
      0.9496924

Spearman's \(\rho\)


      > cor.test(president, prime.minister, method=c("spearman"))

      

              Spearman's rank correlation rho
      

      data:  president and prime.minister
      S = 10, p-value < 2.2e-16
      alternative hypothesis: true rho is not equal to 0
      sample estimates:
            rho
      0.965035

Kendall's \(\tau\)


      > cor.test(president, prime.minister, method=c("kendall"))

      

              Kendall's rank correlation tau
      

      data:  president and prime.minister
      T = 62, p-value = 5.319e-06
      alternative hypothesis: true rho is not equal to 0
      sample estimates:
            tau
      0.8787879

分析結果顯示總統執政滿意度與閣揆施政滿意度高度相關，三種相關係數的大小分別是\(r\)>\(\rho\)>\(\tau\)。\(\rho\)與\(\tau\)的手動計算可以參考Spearman's \(\rho\) Step by Step與Kendall's \(\tau\) Step by Step。

連檢定 Wald-Wolfowitz Runs Test

又稱為隨機性檢定，是檢驗數值發生順序是不是隨機，也就是樣本分布有沒有隨機的方法。連檢定的概念其實不難理解，所謂的「連」指的是同一個數值「連續出現」的意思，連檢定就是計算這個「連續出現」的次數有沒有違反常理。一般來說，如果是隨機分布，同一數值連續出現的次數應該會減少，也就是「連」會顯得比較分散、比較多。例如丟銅板十次：

情況一：正正反正反正反正正反
情況二：正正正反反正正正正反

情況一共有8個連，包含2個正、1個反、1個正、1個反、1個正、1個反、2個正、1個反。

情況二共有4個連，包含3個正、2個反、4個正、1個反。

上述兩種情況不需要統計檢驗，我們用直覺來判斷也可以感覺情況一比較像是隨機分布，情況二比較少見不太像隨機分布。這就是連檢定背後的基本邏輯，也就是判斷「連續出現」的次數有沒有分散或是過於頻繁，太多或太少的「連」基本上都不太符合隨機分布。這個概念是Abraham Wald與Jacob Wolfowitz(1940)發展出來，所以連檢定正式名稱是Wald-Wolfowitz Runs Test。其統計量為：

\[\mu=\frac{2N_{+}N_{-}}{N}+1\]

\[\sigma^2=\frac{2N_{+}N_{-}(2N_{+}N_{-}-N)}{N^2(N-1)}\]

台灣位於歐亞大陸板塊與菲律賓海板塊交界處，地震發生頻繁。氣象局以10年資料統計，台灣每年規模4.0以上的地震約有164次，5.0以上的約有21次，6.0以上約有3次。每次發生地震的時候氣象局都會對外表示「這次地震是正常能量釋放」。所謂的「正常能量釋放」我們可以解讀為地震發生頻率接近隨機。我們就以2021年的地震資料為例，實際以連檢定來看看地震是否是隨機發生。

地震的資料取自中央氣象局地震測報中心。我們將有正式編號的地震，也就是所有測站震度大於4級或兩個以上震度3級以上的地震，依一年365天發生的情況記錄在earthquake.csv，0表示當天沒有地震，1表示當天至少發生一次地震。接著以DescTools套件裡的RunsTest()來測試一年當中地震發生頻率符不符合隨機。


     > earthquake<-read.csv("c:/Users/USER/Downloads/earthquake.csv", header=TRUE, sep=",")

     > str(earthquake)

     'data.frame':   365 obs. of  2 variables:
      $ date      : chr  "1月1日" "1月2日" "1月3日" "1月4日" ...
      $ earthquake: int  0 0 0 0 0 1 1 1 1 1 ...
     > library(DescTools)

     > RunsTest(earthquake$earthquake)

     

             Runs Test for Randomness
     

     data:  earthquake$earthquake
     z = -2.5022, runs = 101, m = 293, n = 72, p-value = 0.01234
     alternative hypothesis: true number of runs is not equal the expected number

可以看到連檢定的結果共有101個連，365天中有72天發生規模較大的地震，293天沒有地震或地震較小，p值<.05，所以我們可以下結論說，當天會不會發生地震是隨機的。接著可以進一步檢驗地震發生的規模是不是也是隨機？我們將2021年台灣發生的496次地震紀錄在earthquake2021.csv。


     > earthquake2021<-read.csv("c:/Users/USER/Downloads/earthquake2021.csv", header=TRUE, sep=",")

     > str(earthquake2021)

     'data.frame':   496 obs. of  7 variables:
      $ 編號    : chr  "小區域有感地震" "小區域有感地震" "小區域有感地震" "小區域有感地震" ...
      $ 地震時間: chr  "2021/1/1 1:42" "2021/1/1 12:57" "2021/1/2 21:26" "2021/1/3 23:09" ...
      $ 經度    : num  122 121 122 122 121 ...
      $ 緯度    : num  24.5 23.6 24.1 24.7 23.8 ...
      $ 規模    : num  4.5 3.2 4.8 3.6 3.9 4.3 4.3 4.1 4.1 4 ...
      $ 深度    : num  65.2 14 25.6 10.3 19.7 13.6 14.1 19.9 12.8 24.2 ...
      $ 位置    : chr  "宜蘭縣政府南方  22.6  公里 (位於宜蘭縣南澳鄉)(宜蘭縣南澳鄉)"
     > RunsTest(earthquake2021$規模)

     

             Runs Test for Randomness
     

     data:  earthquake2021$規模
     z = -2.1062, runs = 222, m = 277, n = 219, p-value = 0.035194
     alternative hypothesis: true number of runs is not equal the expected number
     sample estimates:
     median(x)
           3.9

連檢定結果共有222個連，規模小於中位數3.9的地震共發生277次，大於中位數3.9的地震共發生219次，p值同樣<.05，所以過去一年來地震發生的規模大小也是隨機。RunsTest()決定\(N_{+}\)、\(N_{-}\)的預設切點是中位數，我們也可以用(x>mean(x))的方法改為平均數。


     > RunsTest(earthquake2021$規模>mean(earthquake2021$規模))

     

             Runs Test for Randomness
     

     data:  earthquake2021$規模 > mean(earthquake2021$規模)
     z = -2.1062, runs = 222, m = 277, n = 219, p-value = 0.03519
     alternative hypothesis: true number of runs is not equal the expected number

randtests套件的runs.test()是另一個可以計算連檢定的指令。與RunsTest()相較，runs.test()會排除那些與中位數數值相同的樣本。例如改以runs.test()排除規模3.9的地震後，樣本從本來的496次縮減為460次，連數縮小為207，不過p值仍然達到顯著水準，可見地震規模也是符合隨機分布。


     > library(randtests)

     > runs.test(earthquake2021$規模)

     

             Runs Test
     

     data:  earthquake2021$規模
     statistic = -2.1964, runs = 207, n1 = 219, n2 = 241, n = 460,
     p-value = 0.02806
     alternative hypothesis: nonrandomness

簡介