











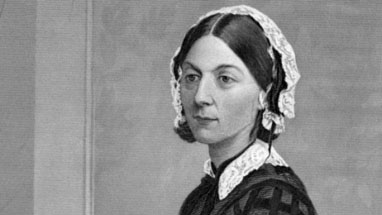







雅各‧伯努利是伯努利家族的一員,伯努利家族一共誕生了八名數學家,堪稱是人類歷史上對數學最具貢獻的家族。 這個家族的起源來自比利時的安特衛普(Antwerp),李奧‧伯努利(Leon Bernoulli)是一名醫生,而他的兒子為了逃避西班牙的宗教迫害,移居到神聖羅馬帝國,整個家族最後在現今的瑞士巴塞爾定居。
雅各‧伯努利是李奧的曾曾曾孫,他的另外兩個弟弟尼可拉斯(Nicolaus Bernoulli)是畫家、約翰‧伯努利(Johann Bernoulli)則是17世紀偉大的數學家。
他是早期微積分的貢獻者,在萊布尼茲(Gottfried_Wilhelm_Leibniz)與牛頓爭執誰才是第一個發明微積分的人,雅各是支持萊布尼茲的。儘管雅各對微積分早期發展有貢獻,但他最為人熟知的還是機率論中的伯努利試驗(Bernoulli trail)以及大數法則(Law of large numbers)。
雅各在只有兩種可能結果的伯努利隨機試驗中,他發現當試驗的次數越多,試驗的結果就會越接近期望值。也就是說當樣本數量夠多的情況下,其平均數就會越接近母體平均,大數法則奠定了日後統計抽樣的原理。
雅各一生的成就都集中在《猜度數》(Ars Conjectandi)這本書中,這本書是在他死後八年才出版。現代數學的伯努利數、伯努利試驗、伯努利多項式等都是紀念雅各當年的數學成就。
雅各出生於瑞士巴塞爾,早年他依循著父親的願望專研神學,但後來對數學的強烈興趣讓他放棄神學這條道路。雅各1687年擔任巴塞爾大學的教授,並開始與他的弟弟約翰共同研究數學,尤其是微積分。但是當約翰的數學才華逐漸展現的時候,開始出現一山不容二虎的氛圍,兩人最終結束了友好的合作關係。
雅各著迷於研究對數螺旋曲線,他最後選擇了這條螺旋曲線當作墓誌銘,同時寫下:Changed and yet the same, I rise again,在巴塞爾大教堂常眠。
資料來源:維基百科他雖然是法國人,但宗教因素讓他最後離開法國轉而在英國定居,也因此認識了牛頓、哈雷等人。
棣美弗出生在法國香檳區,他的父母都是新教徒,法王亨利四世頒布南特敕令(Édit de Nantes)承認宗教自由後,他的孫子太陽王路易十四卻頒布楓丹白露敕令(Edict of Fontainebleau),宣布新教非法,棣美弗因此離開法國。
棣美弗在數學上的貢獻是棣美弗公式,這個公式將複數、三角函數與平面座標結合起來,現在已是高中數學的必學公式。棣美弗也是最早發現斐波納契數列(Fibonacci number)與黃金比例關係的人。然而除了複數的貢獻外,棣美弗也是機率論的創始者之一,今天我們熟知的常態分配其實是棣美弗首次提出。
棣美弗出版了世界第二早的機率論教科書,書名就叫《機率論》(The Doctrine of Chances),這本教科書經過多次再版,棣美弗在書中第一次提到了常態分配的概念,但多數人卻誤以為德國數學家高斯(Carl Friedrich Gauss)才是常態分配的發明者,常態分配也因此被稱為高斯分配,過去德國還未使用歐元以前,馬克紙鈔上還印有高斯以及常態分配的圖像。
在《機率論》這本書中,棣美弗描繪了擲銅板3600次之後出現人頭的機率分布,說明了只要次數夠多,二項分配就會趨近於常態分配。棣美弗的早期論文中也提到了泊松分配(Poisson distribution)的概念,因此也有人認為泊松分配應該是棣美弗分配才對。
資料來源:維基百科約翰·伯努利是雅各‧伯努利的弟弟。他在數學上最大的貢獻除了微積分之外,就是「羅必達法則」(L'Hospital's Rule)。
這個計算極限的簡便方法,是約翰在當羅必達(Guillaume de l'Hôpital)家庭教師的時候教給他的。羅必達1696年出版第一本書中提到這個法則的時候,獲得各界良好的回應,但卻引來約翰的不滿,認為自己的貢獻被羅必達掠奪了。也許羅必達當時覺得付錢請了約翰,兩者並非師徒關係,才認為自己有權利出版學的東西。 儘管這個法則是約翰發明的,但現在世人仍然更熟悉稱為羅必達法則,而不是伯努利法則。
除了與羅必達的不愉快之外,約翰也和自己的親哥哥雅各鬧僵。當年約翰與雅各一起研究數學,但他卻開始忌妒哥哥的數學才華,兩人從合作關係轉變為競爭關係。他們兄弟倆經常研究同一主題,卻也經常產生摩擦。就在雅各死於結核病後,約翰開始把他的忌妒心轉移到自己的兒子丹尼爾‧伯努利(Daniel Bernoulli)上。 在法國巴黎大學的科學競賽上,約翰無法接受與自己的兒子比較的「羞恥」,父子兩人關係降到冰點,約翰甚至將丹尼爾逐出家門。他們父子倆幾乎在同時間發表流體力學研究,約翰還試圖搶先在兒子之前發表,也抄襲了丹尼爾的著作。父子關係最終宣告破裂,直到約翰過世前都未能化解。
與自己的哥哥一樣,約翰也是畢業於巴塞爾大學。當時伯努利家族從事辛香料貿易,父親希望約翰能學習商業管理,但約翰卻對商學沒有任何興趣,最後他說服父親讓他進入醫學系就讀,最終還是因為興趣不合而改走數學這條路,與哥哥一同研究數學。
約翰是萊布尼茲(Gottfried Wilhelm Leibniz)的學生,當然支持自己的老師才是微積分的發明人。也因為伯努利家族支持萊布尼茲,甚至是笛卡耳的渦旋理論(vortex theory),最後也導致整個歐洲大陸在接受牛頓萬有引力定律時,已經落後英國一大截。
他同時也是被譽為最偉大數學家歐拉(Leonhard Euler)的老師。
資料來源:維基百科機率論中著名的「聖彼得堡悖論」(St. Petersburg paradox),最早出現在尼可拉斯一世與法國數學家蒙馬特(Pierre Raymond de Montmort)的通信中。這封1713年9月9日的信中,尼可拉斯一世首次提及這種潛在收益無限大的賭局,到底賭徒願意花多少賭金參與這項賭博?聖彼得堡悖論最後由尼可拉斯的堂兄弟丹尼爾‧伯努利(Daniel Bernoulli),這位曾經去過聖彼得堡教書的數學家提出解釋。
從尼可拉斯提及的聖彼得堡悖論,不難想像他對機率論的貢獻。他對數學的貢獻多半來自與蒙馬特多達560封的通信,這些通信最後被集結出版成冊,書名就叫作《賭博的分析》(Essai d'analyse sur les jeux de hazard)。
除了與蒙馬特通信外,尼可拉斯也與當代大數學家萊布尼茲(Gottfried Wilhelm Leibniz)、歐拉(Leonhard Euler)等人交好。他整理自己的伯父雅各‧伯努利(Jacob Bernoulli)的日記,協助出版《猜度數》(Ars Conjectandi)。由於這本書是在雅各死後八年才出版,因此可以說沒有尼可拉斯,就沒有這本偉大著作。
尼可拉斯一世畢業於巴塞爾大學,他的指導老師其實就是雅各‧伯努利。畢業後他周遊列國,最後在義大利帕多瓦(University of Padua)大學任教幾何學及微積分,1722年才再度回到巴塞爾大學。尼可拉斯一世1714年獲選為倫敦皇家學會院士,也是義大利波隆納學會成員。
尼可拉斯一世與父親同名同姓,他的父親是一名畫家及巴塞爾市議員,是伯努利家族中少數不在數學領域的人,但尼可拉斯一世的伯父雅各及叔叔約翰,都是大名鼎鼎的數學家。
資料來源:MacTutor尼古拉斯二世是約翰‧伯努利(Johann Bernoulli)的兒子,丹尼爾‧伯努利(Daniel Bernoulli)的哥哥。他只活了31歲便英年早逝。他優秀的數理天份受到俄羅斯彼得大帝賞識,受邀到聖彼得堡任教,但只在聖彼得堡待了短短八個月便因為高燒不退撒手人寰。他在俄羅斯的教職最後由大數學家歐拉所取代。
尼可拉斯二世主要的貢獻在於正交軌跡(orthogonal trajectory)、微積分、機率論與流體力學。與家族其他成員一樣,他也與瑞士大數學家歐拉(Leonhard Euler)交好。尼可拉斯二世在巴塞爾大學獲得博士學位後,隨即在威尼斯擔任私人講師,他也是義大利帕多瓦大學(University of Padua)的數學主任。
正當父親與英國數學家泰勒(Brook Taylor)爭論誰才是第一位發表求解「振盪中心」(center of oscillation)方法的時候,尼可拉斯二世很自然地站在父親這邊。在丹尼爾‧伯努利與父親交惡的時候,他也待在父親身旁擔任數學研究的得力助手。
資料來源:維基百科伯努利定律(Bernoulli principle)的發明人,這個在流體力學中重要的定律,證實了流速愈快壓力愈小,現代飛機能飛在空中就是利用這個原理,利用機腹較機背扁平的設計,讓飛機下方的氣壓大於機背,藉此支撐飛機重量。
作為伯努利家族的一員,他不僅是物理學家也是出色的數學家。丹尼爾生於荷蘭格羅寧根(Groningen),當年為了逃避西班牙的宗教迫害,舉家遷往法蘭克福,隨後在瑞士巴塞爾定居。丹尼爾是約翰‧伯努利(Johann Bernoulli)的兒子,父子倆具有相同的數學才華,但一山不容二虎,在一次巴黎大學的科學競賽中約翰羞於和自己的兒子平起平坐,最終將丹尼爾逐出家門。 約翰也抄襲了丹尼爾流體力學的著作,儘管丹尼爾多次向約翰釋出和解善意,但父子倆人的關係絕裂到約翰死前都沒有轉圜餘地。
儘管父子倆人間的隔閡,但卻不容抹滅兩人在數學上的貢獻。父親約翰是早期微積分的奠基者,而丹尼爾則是伯努利定律的發明人。與父親成長的背景如出一轍,或許是出自於約翰早期沒有遵從父親學習商學的期望,約翰起初也是鼓勵丹尼爾學習經商。但就像他的父親一樣,丹尼爾對數學有濃厚興趣,他與父親約翰一樣,拒絕商業管理而改投醫學懷抱,約翰也同意會在其他時間教導丹尼爾數學。 父子倆人早年密切關係,讓誰也沒想到多年後,當丹尼爾展露才華時,兩人的關係會到水火不容的地步。
丹尼爾最終獲得了解剖與植物學的博士學位,也因為他的醫學背景,讓他對測量血壓有極大興趣。他和歐拉(Leonhard Euler)一起測量血流速度與壓力之間的關係,終於發現了流速愈快壓力愈小的伯努力定律。丹尼爾當年利用開放式導管測量血壓的方法,也就是後來醫師利用細小導管扎入動脈後測量血壓的方法。這種侵入式測量直到170年後才有義大利醫師發展出較不疼痛的改良型。
丹尼爾對統計學的貢獻則是1738年的《Specimen theoriae novae de mensura sortis》(Exposition of a New Theory on the Measurement of Risk)。在這本名為一個測量風險新理論展示的書中,丹尼爾提出了「聖彼得堡悖論」(St. Petersburg paradox)的解決方案,也就是後來經濟學效用理論中的風險趨避、風險追求、風險中立的最早模型。
同樣基於醫學背景,丹尼爾1766年對天花發病率及死亡率的統計研究,也替30多年後金納(Edward Jenner)發明牛痘疫苗,證時疫苗功效做了先驅性的啟發。
資料來源:維基百科貝葉斯的中文翻譯名稱許多人感到陌生,但談起「貝氏定理」(Bayes' theorem)應該少有人不知道,貝氏定理在現今統計學上有廣泛的應用,也是高中數學的教材。
他在愛丁堡大學修習邏輯學與神學,由於貝葉斯是新教徒,有一說法是當年新教徒還無法進入牛津或劍橋大學就讀。取得學位之後,貝葉斯在肯特郡的地方教堂擔任牧師。
除了一篇關於微積分的文章:An Introduction to the Doctrine of Fluxions, and a Defence of the Mathematicians Against the Objections of the Author of The Analyst,貝葉斯在生前幾乎沒有發表過任何論文,後是對他的瞭解主要來自於好友普萊斯(Richard Price)在貝葉斯死後整理手稿而得,其中最有名的就是貝氏定理。 這篇名為「機率論一個問題的解決」(An Essay towards Solving a Problem in the Doctrine of Chances),在1763年貝葉斯死後在英國皇家學會發表,並在隔年的自然科學會報,其中包含了貝氏定理的基本命題。
資料來源:維基百科法國著名的數學家、天文學家與物理學家,由於他卓越的貢獻,被喻為法國的牛頓。
拉普拉斯在法國的諾曼第出生,他們家庭早期務農,但他的父親皮耶‧拉普拉斯(Pierre Laplace)也同時是蘋果酒商人。拉普拉斯本來在卡昂大學(University of Caen)修習神學,但後來卻對數學產生興趣,最後他並沒有拿到神學學位。
拉普拉斯的數學與統計思考有很大一部分來自於他的曠世鉅著《天體力學》(Mécanique Céleste),在這本長達五卷的作品中,拉普拉斯探討了星球的形狀、運動以及太陽系的形成與演化,考慮到宇宙中可能存在黑洞,其中最著名的就是探討太陽明天到底會不會升起的機率方程式。
這個名為「連續法則」(rule of succession),拉普拉斯認為如果某一件事情連續發生,那麼它再度發生的機率會是(n+1)/(n+2)。拉普拉斯認為這個公式可以應用在一切未知的事情上,他也將這個公式應用在太陽升起的預測,他預估太陽明天會升起的機率將是(d+1)/(d+2),其中d是一段時間內太陽升起的次數。
儘管這個公式遭受不少爭議,但拉普拉斯對天文物理的研究,卻發展出機率論的概念,從過去事件推估機率的方法,其實就是現代熟知的貝氏機率,最早是由英國牧師貝葉斯所提出,透過拉普拉斯將之發揚光大。
現代所熟知的機率法則,包含兩獨立事件的聯合機率必須相乘,條件機率必須相除的概念,都是由拉普拉斯發展出來。回歸分析最常使用的最小平方法,以及機率論最重要的中央極限定理,都必須回歸到18世紀拉普拉斯最初的貢獻。
拉普拉斯除了對科學與數學的貢獻外,當時他亦結識法國皇帝拿破崙,被任命為法蘭西第一帝國的內政部長,但時間僅有短短六個月。科學家與政治總有隔閡,拿破崙亦坦承這是一個錯誤決定,甚至嘲笑拉普拉斯無法解決問題,只是把無窮小量的數學精神帶入政府部門,明顯認為拉普拉斯不適合從政。
拿破崙失敗波旁王朝復闢後,拉普拉斯被任命為侯爵(marquis)。拉普拉斯生於法國最動盪的時刻,他經歷過法國大革命、拿破崙崛起、波旁王朝復辟,曾有人認為他雖然在科學上取得巨大成功,但在政治上其實是個牆頭草。
拉普拉斯在哲學上提出著名的「拉普拉斯惡魔」(Laplace's demon),他在1814年提到:現在的宇宙是過去的結果,同時也是未來的成因;如果有一種智慧可以知道所有促成與宙運動力量以及物體的位置,同時也能對這些數據進行分析,宇宙中最大的物體與最小的粒子運動都包含在這個簡單的公式中,那麼對這個智慧而言,未來只會像過去一樣出現在他眼前。這段敘述中所描繪的智慧,後人稱之為拉普拉斯惡魔。
拉普拉斯早年離開卡昂大學時,曾帶著一封推薦信去見當時的大物理學家達朗貝爾(Jean le Rond D'Alembert),但卻遭到達朗貝爾拒絕。或許是年輕時曾經吃過大師的閉門羹,拉普拉斯成名後對於後進倒是提攜甚多,包含化學家給呂薩克(Joseph Louis Gay-Lussac)、泊松(Siméon Denis Poisson)和年輕的柯西(Augustin Louis Cauchy)等都曾受惠於拉普拉斯。
資料來源:維基百科普萊菲生於1759年9月22日,卒於1823年2月11日,這位來自蘇格蘭的工程師是現代統計圖的發明人,現代常用的折線圖、長條圖以及圓餅圖都出自普萊菲。
多數人以為圓餅圖是南丁格爾發明的,其實普萊菲在《統計祈禱書》(Statistical Breviary)中畫了全世界第一張圓餅圖,這張圓餅圖描繪的是鄂圖曼土耳其帝國在歐、亞、菲三洲的土地分布。而在他出版的《商業與政治圖集》(The Commercial and Political Atlas)中,也包含了43張折線圖以及一張分析各國進出口狀況的長條圖。
普萊菲不僅是優秀的統計圖專家,也曾經是改良蒸汽機,帶動工業革命的瓦特(James Watt)的助手,更是一名行動派人士,他甚至曾經參與導致法國大革命的攻占巴士底監獄行動。
資料來源:維基百科小學老師為了懲罰調皮搗蛋的高斯,在黑板上出了一道1加到100的難題,沒想到高斯瞬間就給出了5050的答案。這個故事有很多不同的版本,但每一個版本都顯示高斯的數學天分。憑著在代數、幾何、統計的多方面貢獻,高斯被譽為最偉大的數學家。
高斯誕生於一個不算富裕的家庭,他的母親不識字甚至根本不記得高斯的確切生日,只知道兒子是誕生在耶穌升天節前八天的某個星期三。高斯憑著這些資訊用數學方法計算出自己的生日。高斯是數學神童,在三歲時就能指出父親計算錯誤,七歲時發展出等差級數的計算方法,也就是上述故事的來源。
雖然家中不太富裕,但高斯憑著他的天才很快就吸引到普魯士布倫威克公爵(Duke of Brunswick)卡爾斐迪南的注意,布倫威克公爵也成為日後高斯的主要資助人,讓高斯得以進入哥廷根大學就讀。
高斯在數學上首次重大突破是發現正多邊形的邊數是費馬質數與2次方的乘積,這項發現證明多邊形可以透過尺規作圖畫出來,其中最有名的就是正17邊形的作圖方法。
常態分配是高斯在統計學上的重大貢獻,儘管常態分配最早是由棣美佛提出,但受限於缺乏機率密度函數的概念無法進一步解釋。高斯在1823年的著作中介紹了最小平方法、最大概似法以及常態分配等重要統計概念,並選擇了算術平均數作為估計參數,也因此常態分配最常見的另一個名稱就是高斯分配,儘管包含棣美佛、拉普拉斯等人都曾研究過這個分配。
卡爾皮爾森是將常態分配這個術語推廣的重要人物,他將這個分配稱作拉普拉斯—高斯曲線,也稱為常態曲線。
資料來源:維基百科泊松的名字被刻在巴黎艾菲爾鐵塔上,與拉普拉斯、傅立葉齊名,是艾斐爾鐵塔72位科學家之一,可見柏松在法國科學界的地位。
生於1781年6月21,卒於1840年4月25日,是一名軍人之子。泊松在20歲之前就已經在法國科學界嶄露頭角。泊松在法國高等理工學院一年級時就受到高度注目,學校破天荒讓他自由選課。還不到二年級泊松就已經發表兩本備忘錄,一本是關於數學上的消去法,另一本則是有限差分方程(finite difference equation)。泊松獲得拉格朗日(Joseph Louis Lagrange)高度讚賞,也與拉普拉斯情同父子。
泊松擔任過教職,也是法國天文局的天文學家。他的一生共發表300多篇作品,內容涵蓋純數學、應用數學、物理學等。法國數學物理學家阿拉哥(François Arago)曾描述他:一生當中最擅長的就是算數學與教數學。
泊松在統計學上最著名的貢獻就是泊松分配(Poisson distribution),適合於描述單位時間內隨機事件發生的次數的機率分佈,衍生出泊松回歸。除了統計學外,泊松也研究天體運行的軌道,以他名字命名的數學、統計學方法不勝枚舉,甚至月球上的隕石坑也命名為Poisson,以紀念他對人類的貢獻。
資料來源:維基百科南丁格爾在義大利出生,在德國學習護理,並在英國倫敦的醫院擔任護理長。
克里米亞戰爭時,南丁格爾極力向英國軍方爭取在戰地開設醫院,為士兵提供醫療護理。為了說服軍方,她利用圓餅圖分析資料,證明英軍死亡原因是受傷後的感染併發症,真正死在戰場上的人反而不多。
也因為如此,南丁格爾是現代統計圖形的先驅,她的圓餅圖又稱為南丁格爾玫瑰圖(Nightingale rose diagram)。南丁格爾是英國皇家統計學會的第一位女成員,後來成為美國統計協會的名譽會員。
儘管世界最早的圓餅圖並不是南丁格爾發明,一般相信世界最早的圓餅圖出自蘇格蘭的威廉·普萊菲(William Playfair)之手。由於南丁格爾的努力,讓昔日在地位低微的護理師社會地位大為提高,南丁格爾也成為白衣天使的代名詞。
資料來源:維基百科柴比雪夫這位堪稱俄羅斯最偉大的數學家,最大的貢獻是柴比雪夫不等式(Chebyshev inequality),證明了無論資料呈現何種分配,至少有1-1/k^2的數據,落在k個標準差的範圍,說明了幾乎所有的隨機變數都會接近平均數。
柴比雪夫雖然是俄國人,但很早就學習法語,這有助於他未來跟當代的數學家溝通。柴比雪夫的腳有發育不良的毛病,這讓他很少出門與其他孩童嬉戲,更能專心在數學上。他最後在莫斯科大學取得學士學位,也成為莫斯科大學的數學教授,並培育出馬可洛夫(Andrey Markov),也就是馬可洛夫鏈(Markov chains)的發明者,另一名學生李亞普諾夫(Aleksandr Lyapunov)則發展出了李亞普諾夫函數(Lyapunov function),對於微分方程具有重大貢獻。
柴比雪夫被認為是俄國的數學之父,蘇聯曾經在1946年發行過柴比雪夫肖像的郵票,同時月球上其中一個坑洞就是以他的名字來命名,包含火星與木星之間的小行星帶,也有一顆以柴比雪夫命名的小行星,以紀念他在數學上的貢獻。
資料來源:維基百科高爾頓是達爾文的表弟,影響現代統計學最深的皮爾森正是高爾頓的徒弟。他最知名的是提倡優生學。
高爾頓曾經學醫,也在劍橋大學三一學院研究數學,但他主要的興趣在遺傳學,他是首先發現不同人、不同種族有不同指紋的人,這對於後續的刑事犯罪有重大影響。
高爾頓在統計上的貢獻包含他是最早使用問卷測量主觀心理的人,同時為了研究遺傳,高爾頓也在相關分析與回歸分析上做出重大貢獻。高爾頓在他的優生學著作《遺傳的天才》 (Hereditary Genius) 中主張人類的才能夠透過遺傳來延續,他發現身高高的父母所生的小孩會比父母矮,身高矮的父母所生的小孩又比父母高,似乎有某種力量將所有下一代的身高從兩端推向中間。但依照遺傳學卻認為遺傳應該會把優勢傳遞給下一代,如此一來下一代的身高應該會呈現兩極化,而不是向中間靠攏。
為了解答疑惑,高爾頓設計出了「高爾頓板」,也就是現代的彈珠台,只是當年的這項裝置上方是一個漏斗,可以將許多小球倒入任其掉落,小球每碰到一個釘子有50%機率往左、50%機率往右,最後落入底部的凹槽內,而且會呈現常態分配。
如果是把彈珠台從中截斷呢?高爾頓在彈珠台中間設計一個開關讓小球不會繼續往下掉,他發現小球在中間不僅是常態分配,打開開關後讓小球繼續下落,最後也會在底部形成一個常態分配。高爾頓因此結論認為,任何一個因素都不會影響最後的常態分配結果,因此身高一定會符合中央極限定理,高爾頓在1877年發表關於種子的研究結果,指出迴歸到平均值(regression toward the mean)現象的存在,也是迴歸一詞的起源。
高爾頓第一次使用了相關係數(correlation coefficient)的概念。他使用字母「r」來表示相關係數,這個傳統一直延續至今。
資料來源:維基百科現代統計學最重要的貢獻者,同時也在1911年創辦倫敦大學學院統計系─全世界第一個統計系所。
皮爾森對於相關係數、假設檢定、P值、卡方檢定、主成分分析等基礎統計的發展占有一席之地,P值的概念更是在卡方檢定中首次被皮爾森正式以大寫P所定義,卡方檢定、卡方分配正是由皮爾森引入統計領域之中,成為現在分析名目資料最重要的分析方法。
高爾頓(Francis Galton)那裡,皮爾森發展出相關係數的計算方法,如今兩個計量變數關聯性也稱做皮爾森相關係數。同時他也透過計算列聯表中觀察值與期望值的差異,發展卡方檢定,提出配適度檢定的分析方法。
皮爾森除了是一名統計學家之外,他也在劍橋大學國王學院取得數學學士,畢業後赴德國海德堡大學研究物理,並至德國柏林大學學習羅馬法與文學。他對自然科學的主張在《自然的文法》( The Grammar of Science)一書中表露無疑,他認為自然界的規律相對於觀察者的感知能力,甚至宣稱如果人類以光速運動可以超越時空的永恆,這樣的概念也影響後來愛因斯坦發展出相對論。
資料來源:維基百科高塞特在牛津大學學習化學與數學,畢業後赴「健力士」(Guinness)釀酒廠工作,在那裡他發展出t分配。
在愛爾蘭釀酒廠期間,他的工作是找出不同大麥品種對釀酒的影響,在這裡高塞特充分運用統計知識與試誤法。由於在釀酒廠工作,高塞特關心的是小樣本的機率問題,畢竟大麥品種不可能出現大樣本,高塞特因此找上卡爾皮爾森協助處理數學問題,並發展出t分配統計量,但當時這種針對小樣本的統計量並不為人所重視,直到費雪發揚光大後,才有現今的t分配。
高塞特當年發表t分配時,由於健力士不准員工以真實姓名發表研究,因此高塞特只好用筆名「Student」發表這篇統計學上重要的論文《一個平均數中可能的錯誤》(The probable error of a mean)在皮爾森的「生物統計」(Biometrika)期刊上。費雪將高塞特的分配命名為t,Student's t分配從此在統計學上占有一席之地,而費雪之所以對t分配有高度興趣,也在於高塞特的理論契合費雪的自由度理論。
儘管費雪與皮爾森之間的競爭關係,但高塞特倒是與兩者都保持著友好的關係,皮爾森一值在數學上協助高塞特,而費雪更將t分配發揚光大。
資料來源:維基百科變異數分析的發明者,變異數一詞就是由他而來。費雪來自英格蘭,對統計的主要貢獻包含變異數分析、費雪精確性檢定、最大概似法等。他對統計學的貢獻主要來自於研究優生遺傳學的興趣,尤其是他發現統計方法對於解答孟德爾的遺傳問題有很大的幫助,因此發展出許多統計工具。
從童年開始費雪的視力就一直不是很好,這也讓費雪養成不依賴紙筆數學思考的習慣。他畢業於劍橋大學,當時正值第一次世界大戰,費雪一度想從軍報國,卻因為視力太差被打回票,這也讓他回到學術工作。當時費雪曾經有機會加入由卡爾皮爾森主持的高爾頓實驗室,但他考量到自己與皮爾森之間的競爭關係而作罷,而於隨後進入羅森斯德實驗室(Rothamsted Experimental Station)的農業試驗所。
費雪在實驗室發展出了實驗方法,同時發展出F分配,從此奠定他在統計學上的地位。《孟德爾遺傳親代猜想之關聯》( The Correlation Between Relatives on the Supposition of Mendelian Inheritance)發表於1918年,首次使用變異數分析來解答遺傳問題,同時第一次使用變異數這個名詞。
在遺傳生物學方面,1928年的《自然選擇的遺傳理論》( The Genetical Theory of Natural Selection),費學提出了突變對於生物適應的重要性,一旦生物適應環境後也降低突變的可能性,他也認為龐大的族群數量有機會創造更多的變異,因此更能適應生活環境而存活。
費學無疑在學術上有顯著貢獻,但他是個老菸槍,反駁吸菸會導致肺癌的想法,他甚至利用相關分析蘋果進口與離婚率來證明統計相關不代表因果關係,駁斥吸菸與肺癌的關聯性,不免讓外界質疑他接受菸商的資助。同時作為優生遺傳學家,費雪對種族有著某種程度的偏見,他強力主張不同人種存有先天上的差異,甚至反對聯合國教科文組織的種族聲明( UNESCO Statement of Race),認為這是在誤導社會大眾。
費雪晚年移民澳洲阿德雷德,在澳洲度過餘生。
資料來源:維基百科就像是自傳的書名《An Accidental Statistician》一樣,柏克斯有個很不一樣的人生。出生於英國的他,早期並沒有受過正規的數學或統計訓練,最後卻是美國威斯康辛大學麥迪遜分校統計系的創辦人。
柏克斯本來的興趣是化學,早年他在地方汙水工廠工作,當申請上倫敦大學想專研化學的時候,第二次世界大戰爆發,柏克斯被迫加入陸軍。他在陸軍的工作是研究毒氣,為了瞭解毒氣作為生化武器的效果,柏克斯在動物實驗中需要的不是化學知識而是統計。戰爭期間沒有充足人力,也沒有適當課程的情況下,柏克斯自己買了幾本統計書籍來研讀,好讓自己可以解讀動物實驗中的數據。
這段特殊的經歷讓柏克斯在戰後選擇了數學與統計來完成他的學業。最終他在倫敦大學獲得博士學位,指導教授就是卡爾‧皮爾森的兒子伊根‧皮爾森(Egon Pearson)。柏克斯隨後在世界最大的化學公司帝國化學工業(Imperial Chemical Industries)上班,在這期間他請了一年的假前往美國北卡羅萊納州立大學擔任訪問學者,之後再轉往普林斯頓大學。1960年柏克斯來到威斯康辛大學創立了統計系,直到1992年退休。
柏克斯在品質管理、時間序列分析、實驗設計上有顯著貢獻。時間序列分析中的ARIMA模型,基本上就是來自於他,另外還包含Box-Ljung檢定、Box's M檢定。不過柏克斯最為人稱道的還是他留給後世的一段話:所有模型都是錯誤的,但是有一些是有用的(All models are wrong, but some are useful)。
柏克斯有過三段婚姻,其中第二任妻子Joan Fisher就是統計學家Ronald Fisher的女兒,他們兩個還一起寫了費雪的傳記。
資料來源:維基百科2022年以高齡97歲逝世的考克斯,是現代重要的統計學家之一,也是羅吉斯回歸以及用於存活分析的考克斯回歸(proportional hazards model)的發明人。他和柏克斯提出的Box-Cox轉換,則是現今最常用資料轉換技巧,讓分配能夠更接近常態分佈。
考克斯出生於英國伯明罕,他在劍橋大學取得數學碩士、里茲大學(University of Leeds)獲得博士。隨後他在不同研究單位任職,包含羊毛產業研究學會、倫敦帝國學院、劍橋大學、牛津大學等。1988年考克斯成為牛津大學紐菲學院(Nuffield College)院長及統計系教授,並於六年後從牛津大學退休。因為在統計上的卓越貢獻,考克斯於1985年被英國女王伊莉莎白二世封為爵士。
1958年的《The Regression Analysis of Binary Sequences》,考克斯提出了二元隨機變數的羅吉斯回歸,並在1972年的《Regression Models and Life-Tables》提出了「比例風險模型」,也就是存活分析中最常用的一種回歸模型,成為現代醫學與臨床試驗中最常用的統計方法。
資料來源:維基百科