變異數分析ANOVA的全名是Analysis of Variance。雖然名稱叫做變異數分析，但它仍然是比較組與組之間，對於依變數的平均數有沒有差異，所以其實也是平均數分析的一環。平常用來比較平均數差異的t檢定，在碰到樣本超過2組以上(例如：地區分為北中南、分數分為高中低)時，就必須每個配對都做一次t檢定。組別越來越多就得進行\(C_{2}^{k}\)次t檢定。為了避免這個窘境，ANOVA是一個更有效且快速檢驗多組別平均數是否有差異的方法。
變異數分析的原理是比較組間與組內的差異，也就是要讓組間差異越大，組內差異越小，才可以得出有顯著差異的結論。因此有人將組間差異稱為因子差異(treatment)，組內差異視為誤差(error)。
為了讓平均數能比較，變異數分析必須符合三大前提：
- 常態性：樣本必須符合常態分配，也就是分配至少要長得差不多，奇形怪狀的分配是沒辦法比較的。
- 獨立性：樣本要有獨立性，也就是抽樣一定要隨機。
- 同質性：各組變異數必須相等或接近，也就是兩組常態分配曲線的高矮胖瘦要差不多，差太多代表長得不一樣，不一樣的東西怎麼能比較呢。
變異數分析的公式如下：
| 變異來源 | 平方和 SS | 自由度 df | 均方和 MS | F值 |
|---|---|---|---|---|
| 組間變異 | \(SS_{B}=\displaystyle\sum_{i=1}^{k} \displaystyle\sum_{j=1}^{n_{i}}(\overline{Y}_{i}-\overline{\overline{Y}})^2\) (公式1) \(SS_{B}=\displaystyle\sum_{i=1}^{k}n_{i}(\overline{Y}_{i}-\overline{\overline{Y}})^2\) (公式2) |
k-1 | \(MS_{B}=\frac{SS_{B}}{k-1}\) | \(\frac{MS_{B}}{MS_{W}}\) |
| 組內變異 | \(SS_{W}=\displaystyle\sum_{i=1}^{k} \displaystyle\sum_{j=1}^{n_{i}}(Y_{ij}-\overline{Y})^2\) (公式1) \(SS_{W}=\displaystyle\sum_{i=1}^{k}(n_{i}-1)S_{i}^{2}\) (公式2) |
n-k | \(MS_{W}=\frac{SS_{W}}{n-k}\) | |
| 總變異 | \(SS_{T}=SS_{B}+SS_{W}\) | n-1 |
單因子變異數分析 One-Way ANOVA
組間變異、組內變異的計算過程繁複，所幸透過aov()R可以很快計算F值。我們以電視家庭收視率為例，介紹變異數分析的應用。收視率資料來自www1.xkm.com.tw並從中抽取30筆資料整理成tv_rate.csv可供下載。
> rate<-read.csv("c:/Users/USER/downloads/tv_rate.csv", header=TRUE, sep=",")
> str(rate) #觀看資料結構
'data.frame': 30 obs. of 8 variables:
$ Channel : chr "中視" "台視" "東森新" "TVBN" ...
$ Program : chr "中視新聞全球" "台視晚間新聞" "1800東森晚間" "九點熱話題" ...
$ Type : chr "news" "news" "news" "news" ...
$ Schedule: chr "19:00" "19:00" "17:45" "21:00" ...
$ Time : chr "prime" "prime" "normal" "normal" ...
$ Rate : num 2.45 2.18 1.86 1.58 1.56 1.53 1.43 1.23 1.17 1.02 ...
$ CPM : int 67 75 93 118 119 97 108 121 133 241 ...
$ AdvCost : int 33000 33000 35000 37500 37500 30000 31250 30000 31250 49500 ...
> tapply(rate$Rate, rate$Type, mean) #不同節目類型的平均收視率
drama news show & cartoon
0.6357143 1.2121429 0.4711111
> tapply(rate_sample$Rate, rate_sample$Type, var) #不同節目類型的收視率變異數
drama news show & cartoon
0.17372857 0.45691044 0.07116111
常態性檢定
從平均收視率來看，新聞收視率明顯高於其他節目類型，其次是戲劇與綜藝卡通，但這樣的差異在統計上有沒有意義？由於節目類型分為新聞、戲劇、綜藝卡通三種類型，必須要透過變異數分析來比較平均數。此時的自變數是節目類型，應變數是收視率。變異數分析前應先確定資料是否符合常態性、獨立性與同質性假設，所以得先進行常態分配檢定。
> library(dplyr) #載入dplyr套件，以便可以使用group_by()資料分組功能
> rate %>% #三種節目類型收視率的Shapiro常態性檢定
+ group_by(Type) %>%
+ summarize(p_value=shapiro.test(Rate)$p.value)
# A tibble: 3 x 2
Type p_value
1 drama 0.0140
2 news 0.708
3 show & cartoon 0.0528
同質性檢定
> bartlett.test(Rate~Type, data=rate) #三種節目類型收視率的Bartlett變異數同質性檢定
Bartlett test of homogeneity of variances
data: Rate by Type
Bartlett's K-squared = 7.0372, df = 2, p-value = 0.02964
離群值 Outlier
從檢定結果得知，部分資料並不符合常態分配與變異數同質性的假設，因此本例並不適合進行分析。其實樣本是不是常態分配，受到離群值(outlier)的影響很大，所以我們可以透過刪除離群值的方式讓樣本符合常態分配。
> outlier<-boxplot(rate$Rate~rate$Type)$out #從盒鬚圖中尋找離群值
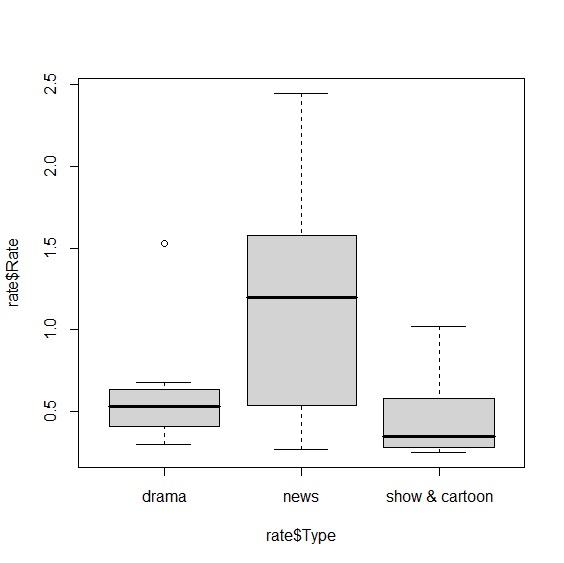> outlier #找到一個drama收視率為1.53的離群值
[1] 1.53
> without_outlier<-rate[-which(rate$Rate %in% outlier),] #刪除離群值
> without_outlier %>% group_by(Type) %>% summarize(p_value=shapiro.test(Rate)$p.value) #常態分配檢定
# A tibble: 3 x 2
Type p_value
1 drama 0.672
2 news 0.708
3 show & cartoon 0.0528
分析結果
為了說明方便，我們還是以原本沒有刪除離群值的檔案，進行後續的單因子變異數分析。
> oneway<-aov(Rate~Type, data=rate) #將ANOVA結果指定給oneway
> summary(oneway) #輸出分析結果
Df Sum Sq Mean Sq F value Pr(>F)
Type 2 3.449 1.7243 6.165 0.00623 **
Residuals 27 7.551 0.2797
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
事後比較 Post hoc
分析結果p值<.05，單因子分析模型達到顯著。但是模型只告訴我們，不同節目類型有不同收視率，卻沒有告訴我們那些節目類型的收視率有差異？也就是那些組別的變數讓ANOVA達到顯著，所以還需要事後檢定才能得知答案。
事後檢定的方法有很多，較常使用的有Scheffe.test與Tukey HSD。Scheffe.test可以同時測試所有可能的配對，最不容易顯著，可用於樣本數不同以及非常態分配上。Tukey HSD測試所有可能pairwise的平均值，樣本數必須一致也必須符合常態分配的假設。為了說明方便，我們兩種方法都採用。
> library(agricolae) #scheffe test在agricolae套件裡，必須先載入agricolae
> scheffe.test(oneway, trt="Type", group=FALSE, console=TRUE) #Scheffe事後檢測
Study: oneway ~ "Type"
Scheffe Test for Rate
Mean Square Error : 0.279685
Type, means
Rate std r Min Max
drama 0.6357143 0.4168076 7 0.30 1.53
news 1.2121429 0.6759515 14 0.27 2.45
show 0.4711111 0.2667604 9 0.25 1.02
Alpha: 0.05 ; DF Error: 27
Critical Value of F: 3.354131
Comparison between treatments means
Difference pvalue sig LCL UCL
drama - news -0.5764286 0.0804 . -1.2104971 0.05763999
drama - show 0.1646032 0.8275 -0.5256832 0.85488960
news - show 0.7410317 0.0108 * 0.1558130 1.32625053
> TukeyHSD(oneway) #TukeyHSD事後檢測
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = Rate ~ Type, data = rate)
$Type
diff lwr upr p adj
news-drama 0.5764286 -0.03056057 1.1834177 0.0651324
show & cartoon-drama -0.1646032 -0.82540925 0.4962029 0.8117987
show & cartoon-news -0.7410317 -1.30125736 -0.1808061 0.0078043
事後檢定顯示news-show & cartoon達到顯著差異。我們可以初步結論，節目型態的收視率有差異，差異主要來自於新聞與綜藝卡通。
雙因子變異數分析 Two-Way ANOVA
在前面的例子中，自變數只有節目類型，當自變數超過一個，例如節目類型與播出時段，這時候就有兩個因子，稱為雙因子變異數分析。手動計算則可參考雙因子變異數分析Step by Step
常態性檢定
延續前面的例子，我們繼續以節目型態與播出時段來說明雙因子變異數分析。正式分析之前，一樣必須先確定資料符合常態性假設。
> rate %>% #節目類型與節目時段收視率的Shapiro常態性檢定
+ group_by(Type, Time) %>%
+ summarize(p_value=shapiro.test(Rate)$p.value)
`summarise()` has grouped output by 'Type'. You can override using the `.groups` argument.
# A tibble: 6 x 3
# Groups: Type [3]
Type Time p_value
1 drama normal 0.292
2 drama prime 0.166
3 news normal 0.378
4 news prime 0.465
5 show & cartoon normal 0.229
6 show & cartoon prime 0.0229
同質性檢定
變異數同質性的部分，除了Bartlett's test之外，這裡介紹另一個常用的方法Levene's test與Fligner-Killeen's Test。兩種檢定方法可用於樣本偏離常態分配的情況。如果有把握樣本接近常態分配，那麼Bartlett's test會是比Levene's test與Fligner-Killeen's Test更好的選擇。
> library(car) #載入car套件
> leveneTest(Rate~Time, data=rate) #Levene變異數同質性檢定
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 1 0.7414 0.3965
28
Warning message:
In leveneTest.default(y = y, group = group, ...) : group coerced to factor.
> fligner.test(Rate~Time, data=rate) #Fligner-Killeen變異數同質性檢定
Fligner-Killeen test of homogeneity of variances
data: Rate by Time
Fligner-Killeen:med chi-squared = 1.4877, df = 1, p-value = 0.2226
Levene或Fligner-Killeen檢定的p值>.05，代表變異數同質。接下來進行雙因子變異數分析。
分析結果
> twoway<-aov(Rate~Type*Time, data=rate) #雙因子變異數分析含Type*Time交互作用項
> summary(twoway)
Df Sum Sq Mean Sq F value Pr(>F)
Type 2 3.449 1.7243 5.878 0.00836 **
Time 1 0.247 0.2466 0.841 0.36829
Type:Time 2 0.265 0.1324 0.451 0.64203
Residuals 24 7.040 0.2933
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
分析結果只有節目型態達到統計顯著，播出時段以及交互作用項皆未顯著。播出時段當作區集(blocking factor)實驗設計的結果，同樣顯示節目型態達到顯著。
> summary(twoway<-aov(Rate~Type+Time, data=rate)) #雙因子變異數分析將Time當作區集
Df Sum Sq Mean Sq F value Pr(>F)
Type 2 3.449 1.7243 6.137 0.00656 **
Time 1 0.247 0.2466 0.878 0.35742
Residuals 26 7.305 0.2810
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> interaction.plot(rate$Time, rate$Type, rate$Rate) #繪製比較圖表
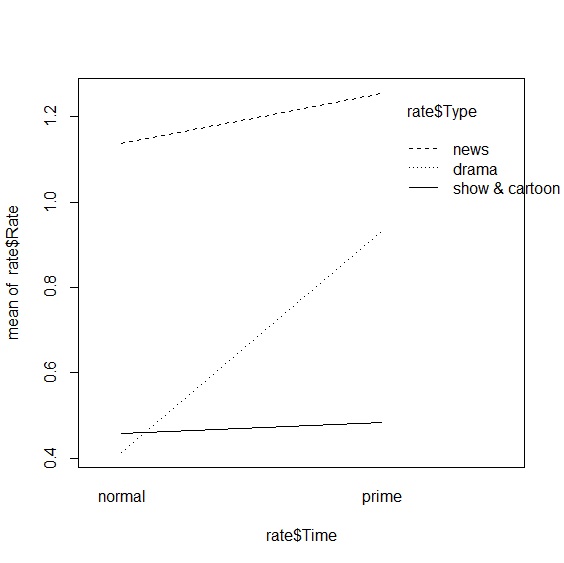
多變量變異數分析 Multivariate ANOVA
無論是單因子還是雙因子變異數分析，應變項都只有一個變數。如果應變數有2個以上，就是多變量變異數分析。例如我們想知道節目型態與收視率還有廣告費之間的關聯，理論上可以作兩次單因子變異數分析，但分析越多次犯下的型I錯誤的機率也越大，所以MANOVA可以在單次分析中涵括所有應變數。
MANOVA的每個自變數，都對應到2個以上的應變數，分析上變成要分析共變數矩陣，計算出矩陣的\(\lambda\)特徵值。由於計算過程繁複，有興趣的人可以參考MANOVA Step by Step，瞭解如何手動計算MANOVA。
回到我們的研究問題：節目型態與收視率、廣告費之間的關聯。R進行MANOVA只要用cbind()指令，先將應變數「集合」起來，再用manova()指令進行分析即可。
MShapiro 常態性檢定
MANOVA必須改用mvnormtest套件中的mshapiro.test()進行常態性檢定。
> y<-cbind(rate$Rate, rate$AdvCost) #結合收視率與廣告費用，創造應變數矩陣
> library(mvnormtest) #載入mvnormtest套件
> mshapiro.test(y) #進行常態分配檢定
Error in mshapiro.test(y) : sample size must be between 3 and 5000 #矩陣行列數不符合程式預設值
> y_trans<-t(y) #將y矩陣轉置
> mshapiro.test(y_trans) #重新進行常態分配檢定
Shapiro-Wilk normality test
data: Z
W = 0.89203, p-value = 0.005391
上述檢定p值<.05，樣本不符合常態分配的假設。由於資料受到離群值(outlier)的影響，我們可以試著找出並刪除離群值，看看離群值對常態分配的影響。離群值分析可以透過mvoutlier套件中的aq.plot()輸出每個變數的布林邏輯值來判斷。
> library(mvoutlier) 載入mvoutlier套件
> outlier<-aq.plot(rate[c("Rate", "AdvCost")]) #繪製outlier圖
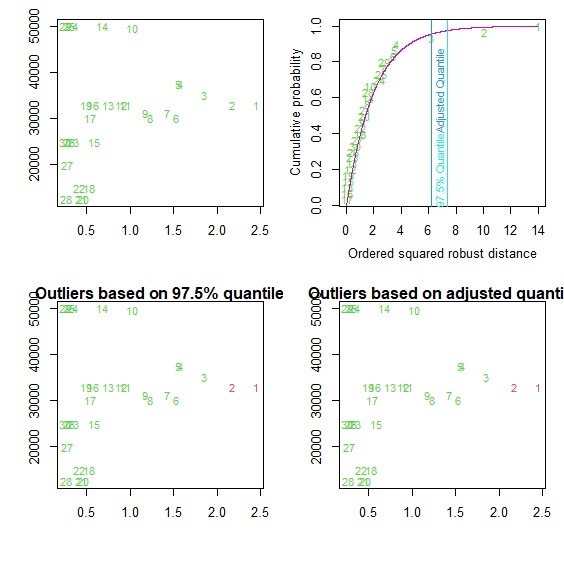> outlier #顯示離群值
$outliers
[1] TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[13] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[25] FALSE FALSE FALSE FALSE FALSE FALSE
Box's M 同質性檢定
上述分析顯示從第1筆與第2筆觀察值是離群值，我們可以刪除這些觀察值後再進行檢定，就可發現檢定力大幅改善。這部分由於過程重複，就不再顯示檢定的結果。這裡只是提醒MANOVA仍要符合常態分配以及變異數同質性的假設。MANOVA因為應變數是矩陣，Box's M是最常用的檢定方法。
> library(heplots) #載入heplots套件
> boxM(y~Type, data=rate)
Box's M-test for Homogeneity of Covariance Matrices
data: Y
Chi-Sq (approx.) = 16.017, df = 6, p-value = 0.01366
Box's M檢定共變數矩陣並不符合同質性假設，但為說明方便，我們還是繼續用本例進行MANOVA。
> manova<-manova(y~Type, data=rate)
> summary(model)
Df Pillai approx F num Df den Df Pr(>F)
Type 2 0.43134 3.7121 4 54 0.009671 **
Residuals 27
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
分析結果
R預設的MANOVA統計檢定是Pillai's trace，其實常用的方法有Pillai, Wilks, Hotelling-Lawley, Roy。可以透過summary()選擇統計方法：
> summary(manova(y~Type), test="Wilks")
> summary(manova(y~Type), test="Hotelling-Lawley")
> summary(manova(y~Type), test="Roy")
上述四種方法都可以計算出統計檢定量，至於哪個方法比較好則是見仁見智，但根據Comparative Robustness of Six Tests in Multivariate Analysis of Variance，Pillai's trace在各種不同情況下會是一個比較穩健(robust)的方法。下面比較四種常見方法：
- —Pillai's trace: \(\displaystyle\sum_{k=1}^{k} \frac{\lambda_{k}}{1+\lambda_{k}}\)，數字越大表示對模型貢獻度越大。
- —Wilk' Lambda: \(\displaystyle\prod_{k=1}^{k} \frac{1+\lambda_{k}}{1}\)，0-1的統計量，與Pillai's trace相反，數字越小表示對模型貢獻度越大。
- —Hotelling's trace: \(\displaystyle\sum_{k=1}^{k}{\lambda_{k}}\)，矩陣特徵值的總和，數字越大表示對模型貢獻度越大，數值通常會大於Pillai's trace。
- —Roy's largest root: \(\lambda_{max}\)，矩陣中最大的特徵值，數字越大表示對模型貢獻度越大，數值通常會小於Hotelling's trace。
追蹤檢驗 Follow-up Analysis
MANOVA結果，節目型態達到統計顯著。接下來我們要問的是，節目型態到底是和哪一個應變數達到顯著？也就是所謂的追蹤檢驗(follow-up analysis)，可以利用summary.aov( )獲得檢定統計量。這裡只顯示Pillai檢定的結果，節目型態與收視率達到顯著，但廣告費則不顯著。
> summary.aov(model, test="Pillai")
Response 1 :
Df Sum Sq Mean Sq F value Pr(>F)
Type 2 3.4487 1.72433 6.1652 0.006231 **
Residuals 27 7.5515 0.27969
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Response 2 :
Df Sum Sq Mean Sq F value Pr(>F)
Type 2 251295238 125647619 0.9776 0.3891
Residuals 27 3470321429 128530423
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> summary.aov(model, test="Wilks")
> summary.aov(model, test="Hotelling-Lawley")
> summary.aov(model, test="Roy")