除了變異數分析留待後續介紹外,平均數檢定使用時機各有不同:
- 單一樣本t檢定:適用於檢定樣本平均數與研究者設定的平均數是否有差異。
- 獨立樣本t檢定:適用於檢定兩組獨立樣本的平均數是否有差異。
- 成對樣本t檢定:適用於檢定兩組相依樣本的平均數是否有差異。
- 變異數分析:適用於檢定三組以上的樣本平均數是否有差異。
無論是哪一種類型的平均數檢定,都需要符合樣本數據呈現常態分配的假設,因此在資料分析之前應該要先做常態分配檢定,以確認可以進行平均數檢定。如果樣本不符合常態分配通常需要進行變數轉換,例如取對數或是開根號,否則就只能改採無母數統計。
成對樣本t檢定
成對樣本適用於比較兩組相依或配對樣本間的平均數差異,例如前測後測、同期比較等。其公式為:
\[t=\frac{\overline{x}_{diff}-\mu}{s_{diff}/\sqrt{n}}\]
\(\overline{x}_{diff}\)=兩個樣本差異的平均值。
\(\mu\)=常數0。
\(s_{diff}\)=兩個樣本差異的標準差。
\(n\)=樣本數。
我們以衛生福利部的門診減量政策為例,用成對樣本t檢定來比較政策施行前後的效果。門診減量政策在2018年7月上路,要求醫學中心與區域醫院,自2018年起逐年減量2%門診,並以五年降低10%為目標。為了比較政策效果,我們從健保署網站院所每月申報點數揭露專區,下載2018年6月(政策推行前)與2019年6月(政策推行後)的「醫院總額各醫院醫療服務點數申報情形」報表,比較兩個時間點醫院門診量有無差異。
相關資料已經整理在nhi_service.csv可直接下載。由於報表是全台灣所有醫院,相當於母體,為了分析方便從中隨機抽樣50個樣本進行分析。
> hospital_population<-read.csv("c:/Users/USER/downloads/nhi_service.csv", header=T, sep=",") #讀取資料
> hospital_population[25, "Before_201806"]<-99 #處理遺漏值
> hospital_population[37, "Before_201806"]<-99 #處理遺漏值
> hospital_population$Before_201806[hospital_population$Before_201806==99]<-NA #處理遺漏值
> hospital_sample<-hospital_population[sample(nrow(hospital_population),50),] #從母體中隨機抽取50個樣本
> dim(hospital_sample) #顯示樣本數,確定抽樣結果
[1] 50 5
> attach(hospital_sample)
> shapiro.test(Before_201806) #常態分配測試,樣本數<50執行Shapiro-Wilk test
Shapiro-Wilk normality test
data: Before_201806
W = 0.84161, p-value = 1.1e-05
> ks.test(Before_201806, "pnorm") #常態分配測試,樣本數>50執行Kolmogorov-Smirnov test
One-sample Kolmogorov-Smirnov test
data: Before_201806
D = 1, p-value = 3.331e-16
alternative hypothesis: two-sided
我們的樣本數有50,應該採用Kolmogorov-Smirnov test。然而無論是採用哪一種方法,都可以看到p<.05,代表樣本不符合常態分配的假設。因此嚴格來說本例不適合t檢定。除了統計檢定外,其實也可以透過Q-Q圖來做tests for normality,如果樣本來自常態分配的母體,則Q-Q圖近似於一條直線。
> qqnorm(Before_201806, main="QQ plot of normal", pch=19) #繪製Q-Q plot
> qqline(Before_201806) #繪製趨勢線
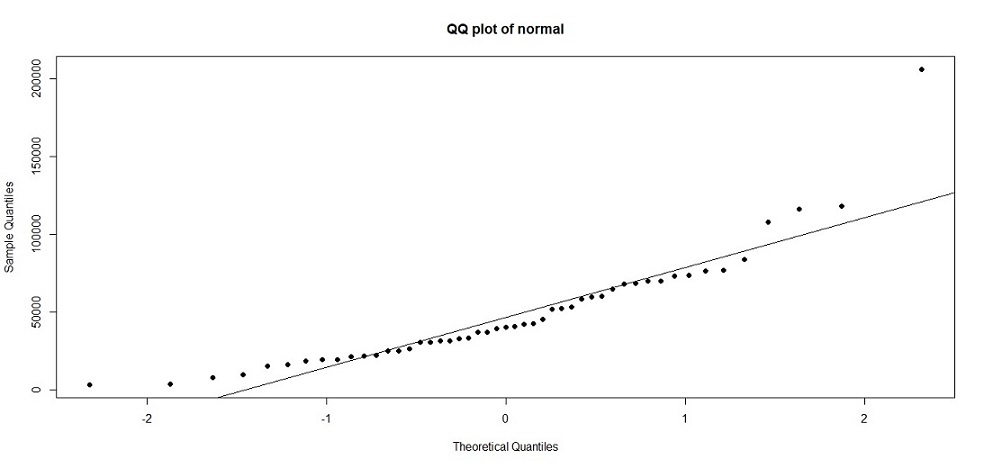
常態分配檢定後,如果樣本符合常態分配(本例不符合)則可進行t檢定。透過設定t.test()的paired=TRUE參數,並用na.action排除遺漏值後,直接進行成對樣本t檢定。
> t.test(Before_201806, After_201906, paired=TRUE, na.action="na.exclude")
Paired t-test
data: Before_201806 and After_201906
t = 2.4666, df = 48, p-value = 0.01726
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
272.9296 2680.1725
sample estimates:
mean of the differences
1476.551
比較2018年6月與2019年6月的西醫門診申報點數後,t檢定小於.05,顯示兩者平均數差異有達到統計顯著。從樣本平均數來看,政策推行後門診申報件數明顯下降,確實有達到門診減量的效果:
> mean(Before_201806, na.rm=T)
[1] 48506.69
> mean(After_201906, na.rm=T)
[1] 46561.88
對照母體實際平均數,可以發現政策施行前的門診申報點數,確實比施行後還多:
> mean(hospital_population$Before_201806, na.rm=T)
[1] 57723.95
> mean(hospital_population$After_201906, na.rm=T)
[1] 55732.47
獨立樣本t檢定
獨立樣本t檢定適用於比較兩組不同樣本之間的平均數有無差異,例如比較男生與女生的成績有無差異、比較都市與鄉村的消費型態有無差異。其公式為:
\[t=\frac{\overline{x}_{1}-\overline{x}_{2}}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\]
\(\overline{x}_{1}, \overline{x}_{2}\)=第一組樣本、第二組樣本的平均數。
\(s_{1}^{2}, s_{2}^{2}\)=第一組樣本、第二組樣本的標準差。
\(n_{1}, n_{2}\)=第一組樣本、第二組樣本的樣本數。
ptt八卦版曾經有人po文詢問「女生很喜歡看中醫嗎?」對於這樣的刻板印象,可以嘗試用獨立樣本t檢定來解答。我們從全民健康保險醫療統計彙整1998年到2019年男女中醫門診的人數,檔案可以從gender_traditionalmed.csv下載。
> trad_med<-read.csv("c:/Users/USER/downloads/gender_traditionalmed.csv", header=T, sep=",") #載入資料
> dim(trad_med)
[1] 22 3
> attach(trad_med)
> shapiro.test(Male) #常態分配測試,樣本數<50執行Shapiro-Wilk test
> shapiro.test(Female) #常態分配測試,樣本數<50執行Shapiro-Wilk test
Shapiro-Wilk test檢測樣本常態分配後可發現男性p值>.05,符合常態分配假設;女性p值<.05,不符合常態分配假設。接下來使用F檢定來看看兩組樣本的母體變異數是否有差異:
> var.test(Male, Female) #檢測變異數是否相等
F test to compare two variances
data: Male and Female
F = 0.16033, num df = 21, denom df = 21, p-value = 9.514e-05
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.06656604 0.38616977
sample estimates:
ratio of variances
0.1603303
F test的p值<.05,拒絕虛無假設,母體變異數不相等。稍後的t檢定必須套用變異數不相等的假設。
> t.test(Male, Female, var.equal=FALSE)
Welch Two Sample t-test
data: Male and Female
t = -17.556, df = 27.565, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1170724.3 -925922.3
sample estimates:
mean of x mean of y
2700413 3748736
t檢定p值小於.05,拒絕虛無假設,男女的平均就醫人數有顯著差異。從平均就醫人數來看,男生2700413人,女生3748736人,女生看中醫的次數確實比男生多。
單一樣本t檢定
當想要知道某一變數的平均數,是否與某個理論值或母體平均數相符的時候,可以採用單一樣本t檢定。公式為:
\[t=\frac{\overline{x}-\mu}{s/\sqrt{n}}\]
\(\overline{x}\)=樣本平均數。
\(\mu\)=母體平均數或理論值。
\(s\)=樣本標準差\(\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^2}{n-1}}\)
\(n\)=樣本數。
近年氣候暖化受到關注。我們以中央氣象局的資料,來驗證冬天是不是越來越熱。氣象局統計,1991年到2020年淡水一月的均溫是15.4℃,我們彙整近10年淡水一月份的氣溫,用單一樣本t檢定來驗證最近這幾年的氣溫,是否與平均溫度有差異。
> year<-c(2012,2013,2014,2015,2016,2017,2018,2019,2020,2021)
> temperature<-c(14.9, 15.6, 16.2, 15.8, 15.8, 17.4, 16.6, 17.6, 16.8, 15.0)
> temp_Jan<-data.frame(year, temperature)
> shapiro.test(temp_Jan$temperature)
Shapiro-Wilk normality test
data: temp_Jan$temperature
W = 0.95122, p-value = 0.6829
Shapiro test樣本符合常態分配,接下來作t檢定。
> t.test(temp_Jan$temperature, mu=15.4)
One Sample t-test
data: temp_Jan$temperature
t = 2.6289, df = 9, p-value = 0.02741
alternative hypothesis: true mean is not equal to 15.4
95 percent confidence interval:
15.50742 16.83258
sample estimates:
mean of x
16.17
近10年淡水的一月平均溫度是16.17℃,明顯高於過去的均溫15.4℃,t檢定的結果p值<.05顯示兩者有顯著差異,冬天確實越來越熱。

