時間序列(time series)是將時間t放在x軸,所對應的資料放在y軸的一組資料序列。分析時是以時間為自變數,各時間點對應的資料為應變數,一般表示式為:
\[y=f(t)\]
既然是依時間所組成的資料,有四個因素會影響時間序列,分別是長期趨勢(trend)、循環變動(cyclical fluctuation)、季節變動(seasonal fluctutation)以及不規則變動(irregular fluctuation),時間序列分析其實就是在拆解這四個因素,以瞭解這四個因素的影響。
- 長期趨勢(T):指資料隨著時間遞移,呈現向上遞增或向下遞減的趨勢。例如物價指數的長期趨勢是呈現上揚。
- 循環變動(C):指資料呈現上下波動的情形。例如景氣循環有高峰、衰退、谷底、復甦的循環。
- 季節變動(S):指資料呈現依週、月、季規律變動的情形。例如旅遊業的旺季是寒暑假,淡季是冬天。
- 不規則變動(I):指資料隨機性的變動。不規則變動是除去長期趨勢、循環變動與季節變動後的隨機項。
依據上述四個因素,時間序列的數學表達式可分為相加模型(additive model)與相乘模型(multiplicative model)
\[\text{相加模型 }Y=T + C + S + I\]
\[\text{相乘模型 }Y=T \times C \times S \times I\]
相加模型假設各組成因素獨立互不影響,但在現實世界中任意因素很難相互獨立,所以經濟分析中多採用相乘模型。一般而言,相加模型適合波動程度或週期變化不隨時間序列變化的資料,反之週期變化隨時間成比例的資料則適合相乘模型。如果沒有特別設定,R預設多半是相加模型,兩者之間可用對數log()來轉換。
\[Y=T \times C \times S \times I\]
\[\log(Y)=\log(T) + \log(C) + \log(S) + \log(I)\]
相加模型:台灣少子化
近年台灣受到少子化的衝擊,新生兒出生數一年比一年少,政府祭出多項措施挽救但這個趨勢短期內看起來仍會持續。我們以台灣少子化來介紹相加模型並預測未來趨勢。2000年到2020年台灣新生兒出生資料來自中華民國統計資訊網,整理好的資料可從這裡直接下載。這是一個從2000年1月到2020年12月,共計橫跨252個月的資料檔。
建構時間序列
ts()是R建構時間序列資料的指令,我們把原本的time變數刪除後重新用ts()讀取newborn建構時間序列,並設定frequency=12表示newborn是一個以月為週期的資料。如果是週資料frequency=52,季資料frequency=4,年資料frequency=1。
> newborn<-read.csv("c:/Users/USER/Downloads/newborn.csv", header=T, sep=",")
> newborn<-newborn[,c("newborn")]
> newbornts<-ts(newborn, frequency=12)
> newbornts
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1 24042 22263 26259 22587 25019 22937 24436 25771 26915 28710 28499 27874
2 23705 21610 22407 20922 21584 19935 20728 22402 18454 25013 22019 21575
3 20931 17551 20185 20565 20603 18137 21093 20365 20735 23175 21120 23070
4 19533 17626 19312 18092 17634 17448 19368 17196 19813 20646 18815 21587
5 16531 17128 18735 17274 16527 16524 16897 17932 18905 19223 20858 19885
⋮
19 17116 13468 16704 13676 15279 13587 14709 15150 13913 16793 16057 15149
20 17139 12497 14567 14285 14587 12886 15104 14330 14533 16236 14687 16916
21 12510 13536 14368 12864 12235 14247 12614 12787 13854 14031 14656 17547
> plot.ts(newbornts)
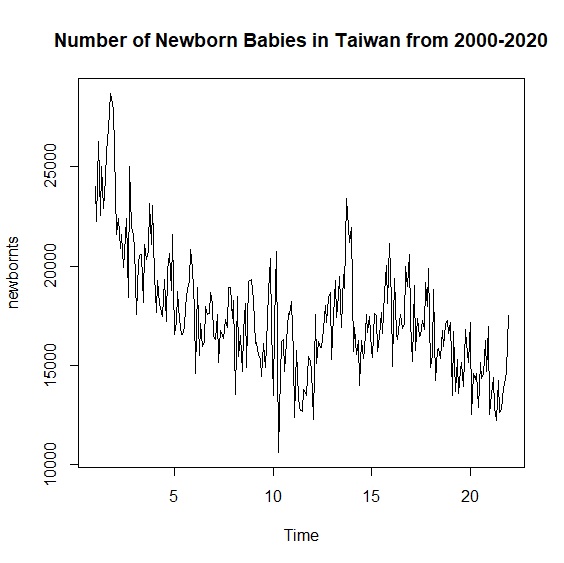
拆解時間序列
時間序列由長期趨勢、循環變動、季節變動與不規則變動四個因素所構成,分析重點在於如何拆解出這些因素。decompose()與stl()兩個指令可以快速拆解出這四個因素,這裡以相加模型來拆解。相乘模型可以設定 type=c("multiplicative")。下面分別比較decompose()與stl()的差異。
> components<-decompose(newbornts, type=c("additive"))
> components_stl<-stl(newbornts, s.window="periodic")
> plot(components)
> plot(components_stl, main="STL decomposition")

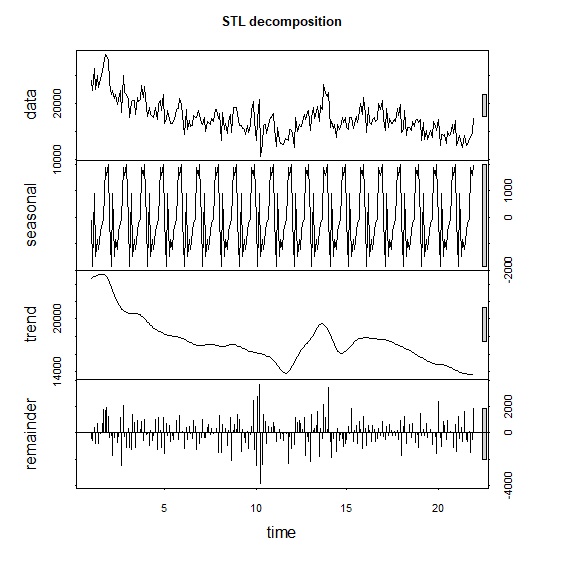
分解時間序列後可以觀察到季節變動的規律性,長期曲線除了2012、2013有反彈回升外整體呈現下滑。2012年正好是龍年,傳統上望子成龍、望女成鳳的觀念讓新生兒出生數出現反彈回升。我們可以將原始資料減去季節變動,獲得季節校正後出生數。
> seasonal_adj_newborn<-newbornts-components$seasonal
預測時間序列
時間序列分析最終目的是希望透過現有資料預測未來,預測時間序列大致有下列方法:
- 移動平均(Moving Average)
在沒有明顯季節變動的前提下,移動平均是最簡單的方法。從1920年代開始移動平均一直是計算時間序列的主要工具,直到現代也常常運用在股市分析。
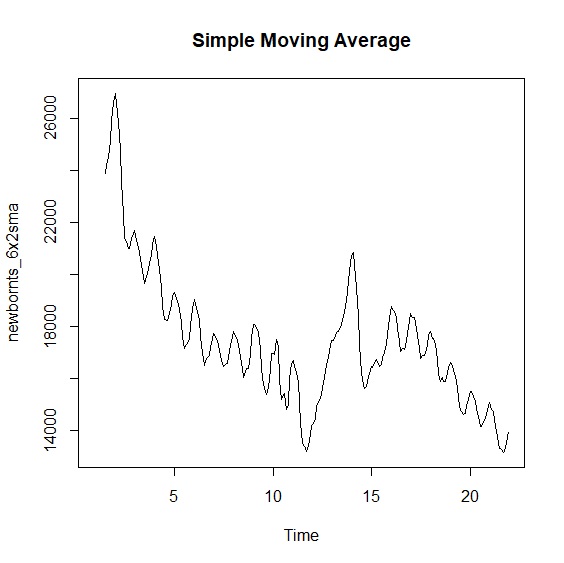
簡單移動平均、加權移動平均、指數移動平均等都包含在TTR套件。我們以SMA()計算週期為6個月的簡單移動平均。週期通常都設為奇數,我們甚至可以計算移動平均的移動平均,也就是將兩個相鄰的移動平均數再平均。指數移動平均則透過EMA()設定平滑參數\(\alpha\),這裡我們設定\(\alpha\)=0.1。
> newbornts_sma<-SMA(newbornts, n=6) #週期6的移動平均
> newbornts_6x2sma<-SMA(newbornts_sma, n=2) #移動平均的移動平均
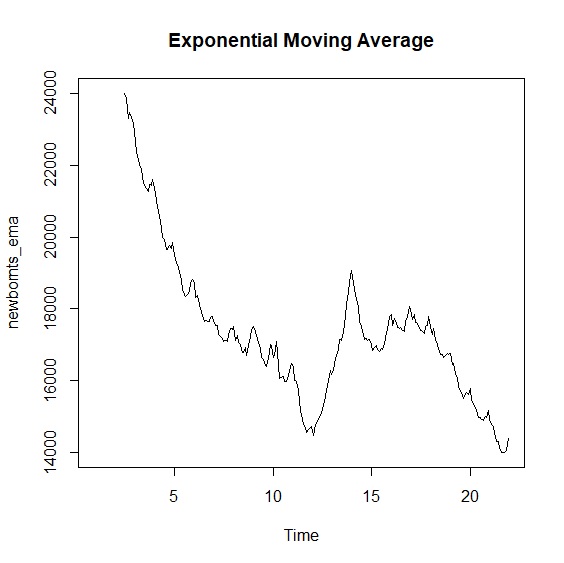
> newbornts_ema<-EMA(newbornts, ratio=0.1) #平滑參數0.1的指數平滑
> plot.ts(newbornts_6x2sma, main="Simple Moving Average")
> plot.ts(newbornts_ema, main="Exponential Moving Average")
- 霍特線性趨勢(Holt Linear Trend Model)與霍特-溫特斯季節趨勢(Holt-Winters Seasonal Model)
美國德州大學奧斯丁分校Charles Holt(1957)將指數平滑法納入趨勢方程式,後來他的學生Peter Winters(1960)將預測方程式改良納入季節因子,最終成為Holt-Winters季節趨勢模型。這個模型是預測時間序列非常著名的方法。
指數移動平均只能掌握時間序列的循環變動而缺乏長期趨勢,霍特的邏輯把時間序列分為循環變化(level)與趨勢變化(trend),將兩者指數平滑後再做線性組合,最後得出一個預測方程式也就是霍特線性趨勢:
\(\text{循環方程式: } l_{t}=\alpha y_{t}+(1-\alpha)(l_{t-1}+b_{t-1})\)
\(\text{趨勢方程式: } b_{t}=\beta(l_{t}-l_{t-1})+(1-\beta)b_{t-1}\)
\(\text{預測方程式: } \hat{y}_{t+h|t}=l_{t}+hb_{t}\)
在霍特線性趨勢的基礎上,溫特斯進一步納入季節週期變動方程式,最終的模型包含\(\alpha\)、\(\beta\)、\(\gamma\)三個參數,分別呈現時間序列的水平、趨勢與季節變動:
\(\text{季節方程式: } s_{t}=\gamma(y_{t}-l_{t-1}-b_{t-1})+(1-\gamma)s_{t-m}\)
\(\text{預測方程式: } \hat{y}_{t+h|t}=l_{t}+hb_{t}+s_{t+h-m(k+1)}\)
上述繁複計算可交由R的HoltWinters()指令來完成。aTSA套件中的Holt()、Winters()也可完成相同工作。R會依據最小平方誤差估計\(\alpha\)、\(\beta\)、\(\gamma\)。HoltWinters()的\(\beta\)與\(\gamma\)參數設定為FALSE,相當於一般的指數平滑法。我們將\(\gamma\)設定為FALSE,保留\(\alpha\)與\(\beta\)進行霍特線性趨勢模型。
> holttrend<-HoltWinters(newbornts, gamma=FALSE)
> holttrend
Holt-Winters exponential smoothing with trend and without seasonal component.
Call:
HoltWinters(x = newbornts, gamma = FALSE)
Smoothing parameters:
alpha: 0.5337442
beta : 0.08048504
gamma: FALSE
Coefficients:
[,1]
a 15974.7164
b 147.8793
接著讓電腦自動計算三個參數建立霍特-溫特斯季節模型,並將模型設為相加模型。
> holtwinters<-HoltWinters(newbornts, seasonal=c("additive"))
> holtwinters
Holt-Winters exponential smoothing with trend and additive seasonal component.
Call:
HoltWinters(x = newbornts, seasonal = c("additive"))
Smoothing parameters:
alpha: 0.3048403
beta : 0.03561554
gamma: 0.2682239
Coefficients:
[,1]
a 13590.56774
b -39.36554
s1 538.77864
s2 -1177.30886
s3 1349.97283
s4 -781.33773
s5 -366.02057
s6 -529.99103
s7 -299.32473
s8 -108.93679
s9 73.03916
s10 1788.24993
s11 1502.90231
s12 2784.92710
比較兩個模型與原始資料的配適差異:
下列方式可以輸出模型的實際配適值與最小平方誤差:
> holttrend$fitted
> holttrend$SSE
> holtwinters$fitted
> holtwinters$SSE
最後可以用forecast套件進行預測。這裡我們以兩個模型預測未來12個月的新生兒出生數,並計算80%與95%的預測區間:
> library(forecast)
> forecast_holttrend<-forecast(holttrend, h=12) #霍特線性趨勢模型預測2021年
> forecast_holttrend
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 22 16122.60 13518.45 18726.74 12139.901 20105.29
Feb 22 16270.48 13264.31 19276.64 11672.944 20868.01
Mar 22 16418.35 13006.46 19830.25 11200.316 21636.39
Apr 22 16566.23 12742.81 20389.66 10718.815 22413.65
May 22 16714.11 12472.10 20956.13 10226.511 23201.71
Jun 22 16861.99 12193.54 21530.44 9722.211 24001.77
Jul 22 17009.87 11906.65 22113.09 9205.170 24814.57
Aug 22 17157.75 11611.14 22704.37 8674.935 25640.57
Sep 22 17305.63 11306.82 23304.44 8131.240 26480.02
Oct 22 17453.51 10993.61 23913.41 7573.949 27333.07
Nov 22 17601.39 10671.48 24531.29 7003.014 28199.76
Dec 22 17749.27 10340.44 25158.09 6418.448 29080.09
> forecast_holtwinters<-forecast(holtwinters, h=12) #霍特-溫特斯季節模型預測2021年
> forecast_holtwinters
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 22 14089.98 12146.44 16033.52 11117.596 17062.37
Feb 22 12334.53 10296.44 14372.62 9217.539 15451.52
Mar 22 14822.44 12687.82 16957.07 11557.820 18087.07
Apr 22 12651.77 10418.69 14884.85 9236.565 16066.97
May 22 13027.72 10694.31 15361.13 9459.075 16596.36
Jun 22 12824.38 10388.82 15259.95 9099.508 16549.26
Jul 22 13015.68 10476.19 15555.18 9131.858 16899.51
Aug 22 13166.71 10521.54 15811.87 9121.273 17212.14
Sep 22 13309.32 10556.78 16061.85 9099.678 17518.96
Oct 22 14985.16 12123.60 17846.73 10608.773 19361.55
Nov 22 14660.45 11688.22 17632.68 10114.817 19206.08
Dec 22 15903.11 12818.62 18987.60 11185.788 20620.43
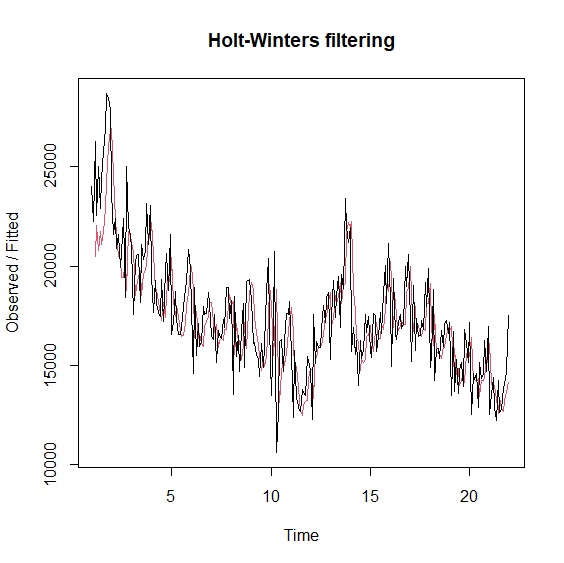
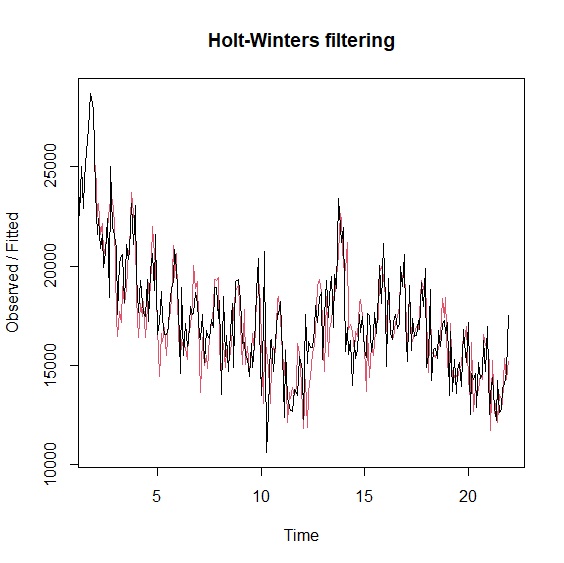
> plot(forecast_holttrend) #霍特線性趨勢模型預測圖
> plot(forecast_holtwinters) #霍特-溫特斯季節模型預測圖
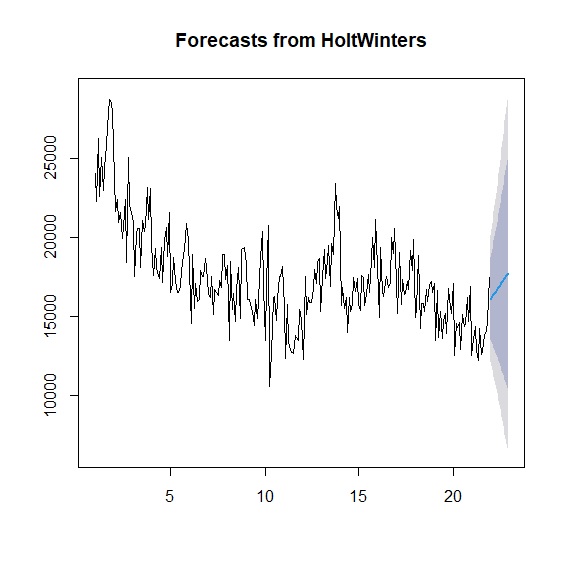
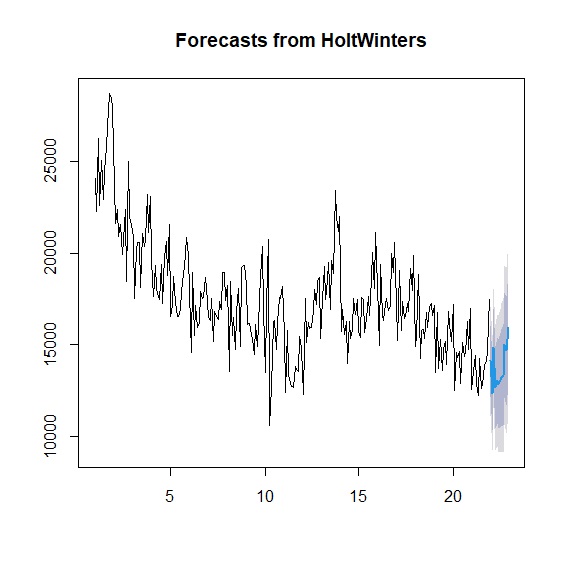
預測的良宥取決於模型與原始資料的殘差,殘差要符合隨機並減少自我相關,這部分的檢定工作可用Ljung-Box來完成。 Ljung-Box<.05表示殘差不是隨機且時間序列中還有模型未解釋的結構。從Ljung-Box檢定來看,無論是霍特線性趨勢、霍特-溫特斯季節模型都還有改善空間。
> Box.test(forecast_holttrend$residuals, lag=20, type="Ljung-Box")
Box-Ljung test
data: forecast_holttrend$residuals
X-squared = 91.673, df = 20, p-value = 3.774e-11
> Box.test(forecast_holtwinters$residuals, lag=20, type="Ljung-Box")
Box-Ljung test
data: forecast_holtwinters$residuals
X-squared = 35.361, df = 20, p-value = 0.01826
- 狀態空間模型(State Space Model)
指數平滑有長期趨勢與季節變動,如果再加上長期衰退(damped)校正因子,搭配相加模型與相乘模型,組合起來至少共有15種類型:
| 趨勢因子 | 季節因子 | ||
|---|---|---|---|
| 無(None) | 相加(Additive) | 相乘(Multiplicative) | |
| 無(None) | N,N | N,A | N,M |
| 相加(Additive) | A,N | A,A | A,M |
| 相加+衰退(Additive damped) | Ad,N | Ad,A | Ad,M |
| 相乘(Multiplicative) | M,N | M,A | M,M |
| 相乘+衰退(Multiplicative damped) | Md,N | Md,A | Md,M |
這麼多模型該如何選擇?狀態空間模型讓一次分析可以直接組合不同因素,R會自動判別最適模型。狀態空間模型來自於兩篇重要的論文Ord, Koehler and Snyder(1997)與Hyndman, Koehler, Snyder and Grose(2002)。事實上R的forecast()預設就是狀態空間模型。
ets()是R的狀態空間模型指令,字母分別代表相加或相乘誤差(Error)、趨勢(Trend)與季節(Seasonal)。ets()不會直接計算預測值,而是告訴我們哪一個模型最適合以及相對應的參數。例如在新生兒出生數的例子中,執行ets(newbornts)時會輸出以下報表透露(M,N,M)是最佳預測模型:
> ets(newbornts)
ETS(M,N,M)
Call:
ets(y = newbornts)
Smoothing parameters:
alpha = 0.3031
gamma = 5e-04
Initial states:
l = 23592.3151
s = 1.1216 1.0805 1.1126 0.98 0.9723 0.9599
0.9421 0.9493 0.9194 1.0623 0.9017 0.9983
sigma: 0.0785
AIC AICc BIC
5047.132 5049.166 5100.073
根據ets()我們的(M,N,M)其實是相乘模型,\(\alpha\)=0.3031、\(\gamma\)=0.0005,沒有趨勢方程式:
\(\text{循環方程式: } l_{t}=(l_{t-1}+b_{t-1})(1+\alpha\epsilon_{t})\)
\(\text{趨勢方程式: } b_{t}= 無\)
\(\text{季節方程式: } s_{t}=s_{t-m}(1+\gamma\epsilon_{t})\)
\(\text{預測方程式: } \hat{y}_{t}=(l_{t-1}+b_{t-1})s_{t-m}(1+\epsilon_{t})\)
預測未來12個月的新生兒出生數:
> forecast_ets<-forecast(newbornts, h=12)
> forecast_ets
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 22 14102.37 12683.23 15521.51 11931.98 16272.75
Feb 22 12737.53 11397.81 14077.24 10688.61 14786.44
Mar 22 15007.14 13363.27 16651.02 12493.05 17521.23
Apr 22 12988.57 11511.31 14465.84 10729.29 15247.85
May 22 13412.26 11832.50 14992.02 10996.23 15828.29
Jun 22 13308.42 11688.77 14928.07 10831.38 15785.46
Jul 22 13563.34 11861.17 15265.50 10960.09 16166.58
Aug 22 13737.51 11962.83 15512.18 11023.37 16451.64
Sep 22 13845.81 12007.48 15684.13 11034.32 16657.29
Oct 22 15715.05 13573.62 17856.47 12440.02 18990.07
Nov 22 15266.05 13133.77 17398.33 12005.01 18527.09
Dec 22 15843.92 13578.18 18109.67 12378.76 19309.08
> plot(forecast(newbornts, h=12))
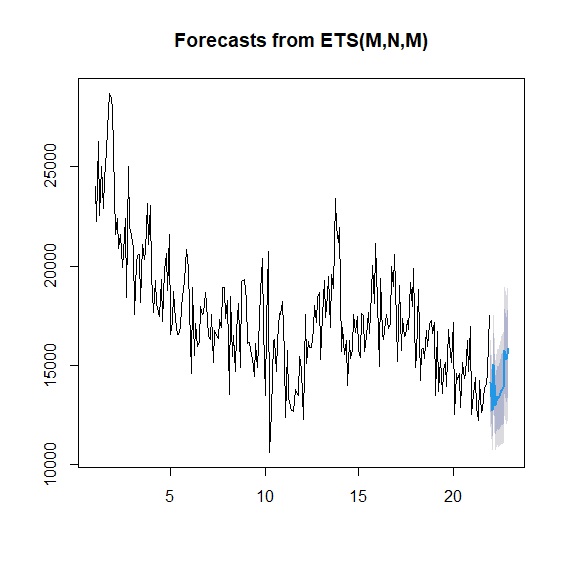
- ARIMA
指數平滑不考慮資料在時序上的自我相關,但有時候將相關性納入考量後可獲得更好的預測。換句話說指數平滑法比較重視數據趨勢和季節性的描述,ARIMA則是描述數據間的相關性。ARIMA是結合自回歸(Auto Regression)與移動平均(Moving Average)模型的簡稱,正式名稱是「自回歸整合移動平均模型」(Auto Regressive Integrated Moving Average),其方程式表示如下:
AR= \(y_{t}=c+p y_{t-1}+p y_{t-2}+\dots+p y_{t-p}+\epsilon_{t}\)
MA= \(y_{t}=c+\epsilon_{t}+q_{1}\epsilon_{t-1}+q_{2}\epsilon_{t-2}+\dots+q_{p}\epsilon_{t-p}\)
ARIMA= \(y_{t}=c+p y_{t-1}+\dots+p y_{t-p}+q_{1}\epsilon_{t-1}+\dots+q_{p}\epsilon_{t-p}+\epsilon_{t}\)
由於ARIMA是將AR與MA兩個方程式相加,所以AR與MA有幾個係數項會影響最終ARIMA模型。ARIMA的係數由p、d、q決定,一般簡寫為ARIMA(p,d,q)。納入季節分析時則簡寫為ARIMA(p,d,q)(P,D,Q)m。
p=自我回歸模型的項數
d=資料差分的次數
q=移動平均模型的項數
m=季節週期
ARIMA建立在平穩型時間序列(stationary time series)的基礎上。也就是沒有長期趨勢與季節變動,只有循環變動的時間序列。因此如果並非平穩型時間序列,必須先用對資料進行差分(differencing)─也就是計算相鄰觀察值的差─獲得平穩時間序列後才可進行ARIMA。
以台灣新生兒出生數為例,這個時間序列有長期趨勢與季節變動,因此用diff()對資料進行差分。我們要建立季節ARIMA模型,先對資料季節差分後再次進行一階差分。如此ARIMA模型為ARIMA(p,1,q)(P,1,Q)12。雙重差分後的資料如下:
> seasonal_diff<-diff(newbornts, differences=12) #季節差分
> double_diff<-diff(seasonal_diff, differences=1) #一階差分
> plot(seasonal_diff, main="Seasonal Difference")
> plot(double_diff, main="Further First Difference")
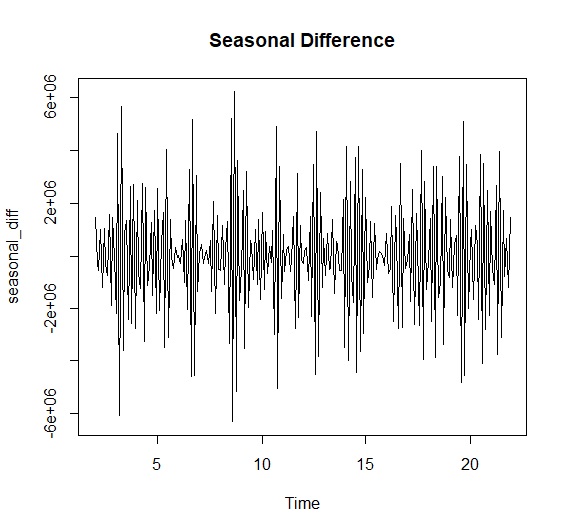
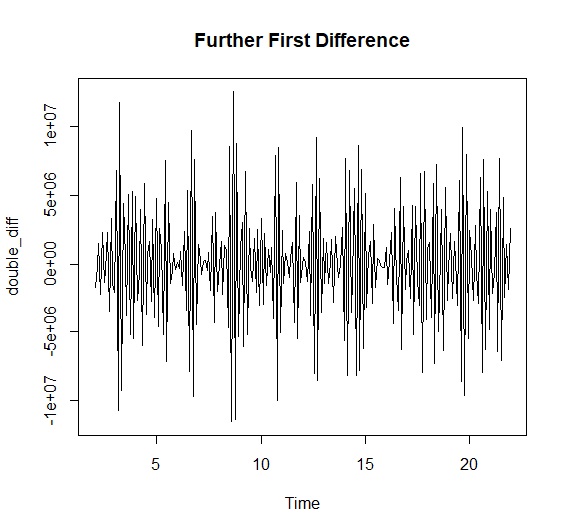
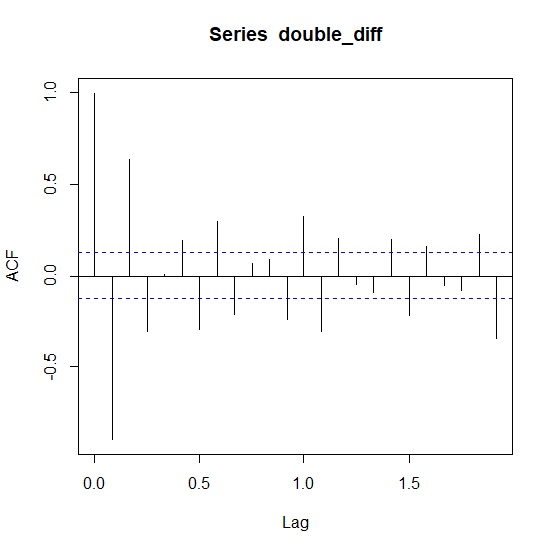
接下來的工作是要決定p、q的數字到底是多少,也就是AR與MA的方程式項數。一個簡單的方法是用自我相關函數來判斷q,偏相關函數圖形來判斷p。acf()與pacf()指令可以繪製圖形。
觀察acf圖在第1個延遲序列與第12個延遲序列後,都至少有3個點超過顯著範圍而沒有明顯收斂,意味著非季節MA的q≥3、季節MA也是Q≥3。一般而言ARIMA的項數不宜超過3,所以如果從acf來決定模型應該是ARIMA(0,1,3)(0,1,3)12。
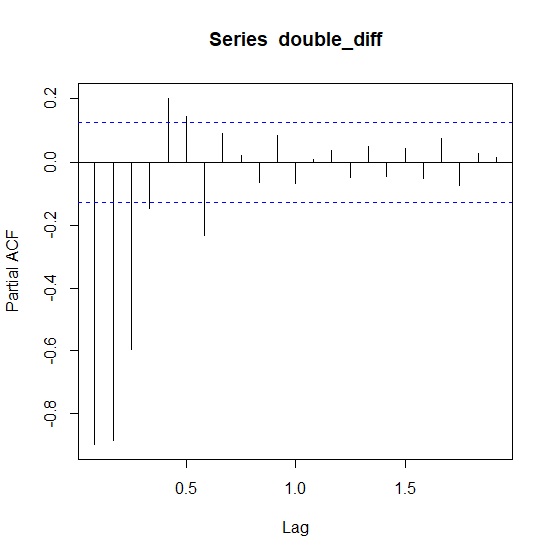
同樣地,pacf圖在前3個延遲序列之後大致都收斂到顯著範圍內,第12個延遲序列後則全部都在顯著範圍內,意味著非季節AR的p=3、季節AR的P=0,模型可設為ARIMA(3,1,0)(0,1,0)12。
兩個模型到底該怎麼選?一個黃金準則是以簡馭繁,所以我們選擇較簡單的模型,ARIMA(3,1,0)(0,1,0)12是我們最後決定的模型。以arima()手動設定相關參數後可以看到模型完整全貌:
> newbornts_arima<-Arima(double_diff, order=c(3,1,0), seasonal=list(order=c(0,1,0),period=12))
> newbornts_arima
Call:
arima(x = double_diff, order = c(3, 1, 0), seasonal = list(order = c(0, 1, 0), period = 12))
Coefficients:
ar1 ar2 ar3
-2.4304 -2.2388 -0.7830
s.e. 0.0421 0.0766 0.0425
sigma^2 estimated as 1.408e+12: log likelihood = -3485.54, aic = 6979.08
AIC=6979.08 AICc=6979.26 BIC=6992.76
這個模型有3個AR係數項沒有任何MA係數,ARIMA(3,1,0)(0,1,0)12的方程式為:
\[y_{t}=-2.43 y_{t-1}-2.24 y_{t-2}-0.78 y_{t-3}+1.408 \times 10^{12}\]
事實上我們也可以用auto.arima()讓R自行決定p、d、q。auto.arima()決定的模型是ARIMA(3,1,0)(2,0,0)12,與我們人工判斷的差異在於季節項。R自行計算的ARIMA不進行季節差分,而且有2個季節自回歸係數,AIC比我們自己判斷的模型更小,數據上來看是更好的模型。
> newbornts_autoarima<-auto.arima(newbornts)
Series: newbornts
ARIMA(3,1,0)(2,0,0)[12]
Coefficients:
ar1 ar2 ar3 sar1 sar2
-0.7500 -0.4998 -0.0917 0.3404 0.3552
s.e. 0.0651 0.0764 0.0645 0.0612 0.0651
sigma^2 estimated as 2465516: log likelihood=-2204.67
AIC=4421.34 AICc=4421.68 BIC=4442.49
ARIMA模型可以進行預測。因為auto.arima()的模型較佳,因此我們直接用這個模型來預測未來12個月的新生兒數。
> forecast_arima<-forecast(newbornts_autoarima, h=12)
> forecast_arima
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 22 14337.13 12324.84 16349.42 11259.601 17414.66
Feb 22 13493.87 11419.65 15568.09 10321.630 16666.11
Mar 22 15152.95 12985.36 17320.54 11837.911 18467.99
Apr 22 14053.87 11621.14 16486.60 10333.331 17774.40
May 22 13950.27 11381.99 16518.54 10022.420 17878.11
Jun 22 14213.17 11527.55 16898.78 10105.876 18320.46
Jul 22 14351.48 11515.66 17187.31 10014.460 18688.51
Aug 22 14114.32 11150.56 17078.09 9581.632 18647.01
Sep 22 14595.57 11515.31 17675.84 9884.709 19306.44
Oct 22 15245.41 12044.92 18445.91 10350.680 20140.14
Nov 22 14898.43 11583.82 18213.03 9829.174 19967.68
Dec 22 16684.85 13261.89 20107.81 11449.891 21919.81
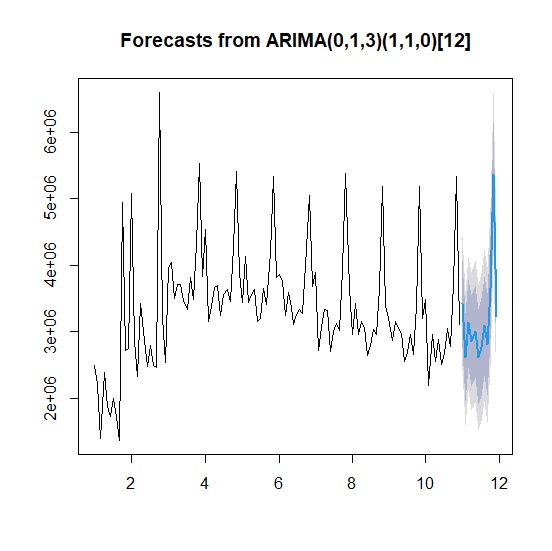
> plot(forecast_arima)
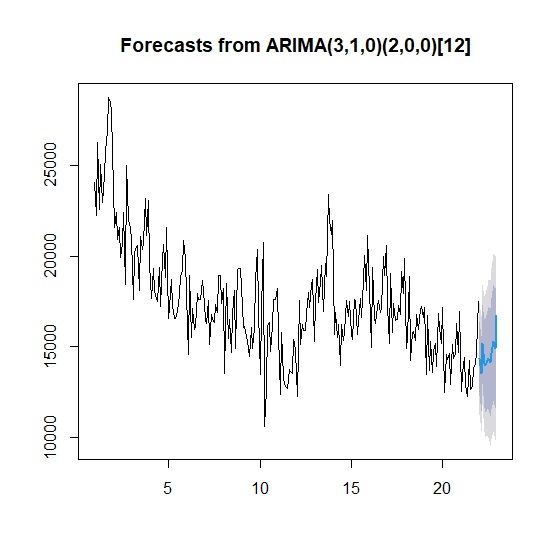
模型殘差Ljung-Box檢測結果<.05,顯示整體模型確實較指數平滑好上許多。
> Box.test(forecast_arima$residuals, type="Ljung-Box")
Box-Ljung test
data: forecast_arima$residuals
X-squared = 0.0012394, df = 1, p-value = 0.9719
驗證分析結果
我們以內政部公布的實際新生兒出生資料,來驗證上述各模型的預測結果。目前公布的資料還缺乏2021年12月份的出生數,所以將12月設為遺漏值。我們以各模型的預測平均數當作基準與實際出生數作比較,並繪製折線圖來觀察預測與實際的差別。
> ActualData<-ts(c(9601,11497,13819,12264,12300,15128,11809,12588,13464,13166,14057,NA), start=22, frequency=12) #2021年實際出生數
> Holt<-forecast_holttrend$mean #霍特線性趨勢預測平均數
> HoltWinters<-forecast_holtwinters$mean #霍特-溫特斯模型預測平均數
> ETS<-forecast_ets$mean #狀態空間模型預測平均數
> ARIMA<-forecast_arima$mean #ARIMA預測平均數
> ts.plot(ActualData, Holt, HoltWinters, ETS, ARIMA,
+ gpars=list(col=c("black", "blue", "red", "green", "purple")))
> legend("bottomright", legend=c("Actual Data","Holt Trend","Holt Winter","ETS","ARIMA"),
+ col=c("black","blue","red","green","purple"), lty=1)
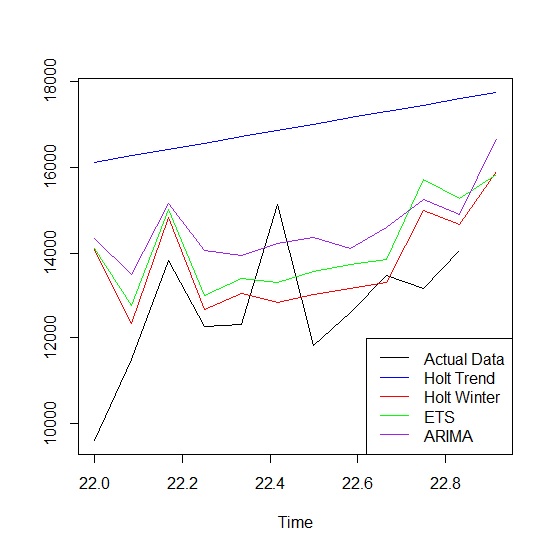
從上圖可以發現預測與實際有不小落差,造成落差的主要原因在於沒有任何模型預測到1月出生數跌破萬人,同時我們只使用預測平均並沒有考慮預測區間。從預測平均來看,霍特-溫特斯季節模型似乎比較符合實際情況。這也說明了ARIMA與狀態空間模型不一定比較準確,畢竟預測這項工作本來就有高度不確定性,模型只是輔助讓預測更有信心、更接近真實而已。下方列出2021年的實際資料與各模型預測平均值。
> comparison<-cbind(ActualData, Holt, HoltWinters, ETS, ARIMA)
> comparison
ActualData Holt HoltWinters ETS ARIMA
Jan 22 9601 16122.60 14089.98 14102.37 14337.13
Feb 22 11497 16270.48 12334.53 12737.53 13493.87
Mar 22 13819 16418.35 14822.44 15007.14 15152.95
Apr 22 12264 16566.23 12651.77 12988.57 14053.87
May 22 12300 16714.11 13027.72 13412.26 13950.27
Jun 22 15128 16861.99 12824.38 13308.42 14213.17
Jul 22 11809 17009.87 13015.68 13563.34 14351.48
Aug 22 12588 17157.75 13166.71 13737.51 14114.32
Sep 22 13464 17305.63 13309.32 13845.81 14595.57
Oct 22 13166 17453.51 14985.16 15715.05 15245.41
Nov 22 14057 17601.39 14660.45 15266.05 14898.43
Dec 22 NA 17749.27 15903.11 15843.92 16684.85
相乘模型:百貨公司周年慶
指數平滑、ARIMA等方法是現今廣受歡迎的時間序列預測法,同時利用decompose()、stl()等指令R可以快速拆解四個因素。這裡我們以林惠玲、陳正倉在《應用統計學》教科書中介紹的古典時間序列分析法,來介紹相乘模型並依步驟人工拆解四個因素。
每年10月到12月年底是百貨公司周年慶,這段時間適逢光輝十月、雙11與聖誕節,一直是各大百貨公司衝刺營收的季節。我們好奇的是購物季對於百貨公司營業額有什麼樣的影響?以遠東百貨為例全台共有11家分店分布在北中南東,是台灣三大百貨龍頭之一。我們以遠東百貨在公開資訊觀測站的財報為基礎,擷取2011年到2020年共計10年的營業收入進行分析。整理好的資料可以直接在這裡下載。資料讀取如下,單位為千元:
> revenue<-read.csv("c:/Users/user/Downloads/fareastern.csv", header=T, sep=",")
> head(revenue)
time revenue
1 11-Jan 2493469
2 11-Feb 2215337
3 11-Mar 1400685
4 11-Apr 2393033
5 11-May 1878665
6 11-Jun 1737501
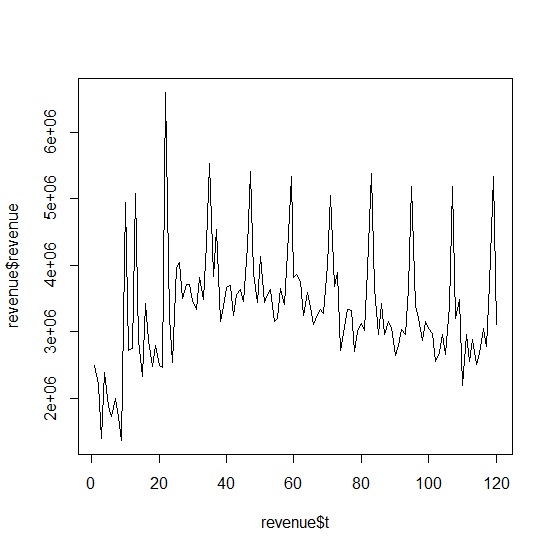
revenue是一個包含120筆記錄的時間序列資料。為進行時間序列分析,增加一個編號1到120的t時間變數,用來表示各時間的營業收入資料點:
> t<-c(1:120)
> revenue<-cbind(revenue, t)
> head(revenue)
time revenue t
1 11-Jan 2493469 1
2 11-Feb 2215337 2
3 11-Mar 1400685 3
4 11-Apr 2393033 4
5 11-May 1878665 5
6 11-Jun 1737501 6
觀察plot()繪製的時間序列可以發現,遠東百貨的營業收入有明顯季節起伏,長期趨勢在最近幾年些微下滑但還算平穩。因為季節變動明顯,所以這不是一個平穩型的時間序列,同時季節變動沒有隨時間成比例,所以也適用於相加模型。
長期趨勢
要估計時間序列的長期趨勢,其實就是找出一條回歸線。這裡我們用簡單線性回歸來找出遠東百貨營業額的長期趨勢。
> trend<-lm(revenue~t, data=revenue)
> trend
Call:
lm(formula = revenue ~ t, data = revenue)
Coefficients:
(Intercept) t
3260076 1692
根據回歸模型,我們可以得出遠東百貨營業額長期趨勢線為y=1692t+3260076。回歸模型透露,隨著時間推移自2011年起遠東百貨每年營業額增加1,692千元。
循環變動
已知長期趨勢\(\hat{Y}\)後根據相乘模型\(Y=\hat{Y} \times C \times S \times I\),公式經過移項後循環變動可表示為:
\[C \times S \times I=\frac{Y}{\hat{Y}}\]
在沒有季節變動,例如年資料,或是不考慮季節變動的時候,我們可以刪除S,所以循環變動與不規模變動可表示為:
\[C \times I=\frac{Y}{\hat{Y}}\]
循環變動與不規則變動是以實際營業額除以預測營業額來衡量。當數值大於1的時候,循環與不規則變動大於長期趨勢;反之則小於長期趨勢。在有季節變動的時候,循環與不規則變動可以與季節變動一起考量。因此接下來我們來分解季節變動。
季節變動
原始資料沒有季營收,所以分析季節變動前得先手動計算遠東百貨的季營業額。一年共4季,從2011年到2020年共有40季的營業額,只需將每3個月的營收相加就能計算出季營收。
> seasonal_revenue<-colSums(matrix(revenue$revenue, nrow=3))
> seasonal_revenue
[1] 6109491 6009199 5101231 10420728 10266411 8772299 7754131 12335224
[9] 11517708 10896653 10632521 13706045 11072973 10615980 10648762 13590122
[17] 11025307 10362100 10260305 13357659 10874476 10064518 9850916 12748750
[25] 9680792 9348923 9143721 12999668 9342711 8859550 8773507 12233554
[33] 9225858 8569486 8305841 11766113 8631254 7948294 8497408 12172036
計算出季營業額後,現在可以開始逐步拆解季節變動。根據相乘模型,季節變動與不規則變動可表示為:
\[S \times I=\frac{Y}{T \times C}\]
公式表明如果能計算出長期趨勢與循環變動,就能分離出季節與不規則變動。那麼該如何計算長期趨勢與循環變動呢?一個簡單方法是計算季資料的移動平均,因為資料平滑後就相當於消除季節與不規則成分,只留下長期趨勢與循環變動。
我們計算4期簡單移動平均數,這項工作可由TTR套件裡的SMA()來完成。
> library(TTR)
> seasonal_sma<-SMA(seasonal_revenue, n=4)
> seasonal_sma
[1] NA NA NA 6910162 7949392 8640167 9303392 9782016
[9] 10094841 10625929 11345527 11688232 11577048 11506880 11510940 11481959
[17] 11470043 11406573 11309459 11251343 11213635 11139240 11036892 10884665
[25] 10586244 10407345 10230547 10293276 10208756 10086413 9993859 9802331
[33] 9773117 9700601 9583685 9466825 9318174 9162876 9210767 9312248
一般而言為了資料對稱,移動平均期數都設定為奇數。這裡的期數4為偶數,所以接著再將兩兩移動平均相加,計算移動平均的移動平均,也就是中央移動平均數。最終可以獲得2011年第三季開始的季節中央移動平均數。這串移動平均數就是萃取出來的長期趨勢與循環變動。
> seasonal_cma<-SMA(seasonal_sma, n=2)
> seasonal_cma<-seasonal_cma[-c(1,2)]
> seasonal_cma
[1] NA NA 7429777 8294780 8971780 9542704 9938428 10360385
[9] 10985728 11516879 11632640 11541964 11508910 11496450 11476001 11438308
[17] 11358016 11280401 11232489 11176437 11088066 10960779 10735455 10496795
[25] 10318946 10261911 10251016 10147584 10040136 9898095 9787724 9736859
[33] 9642143 9525255 9392499 9240525 9186821 9261508
比較原始季營收與移動平均調整後保留長期趨勢與循環變動的季營收如下:
> plot(seasonal_revenue, type="l")
> lines(seasonal_cma, type="l", col="red")
> legend("bottomright", legend=c("Seasonality", "Moving Average"), col=c("black", "red"), lty=1)
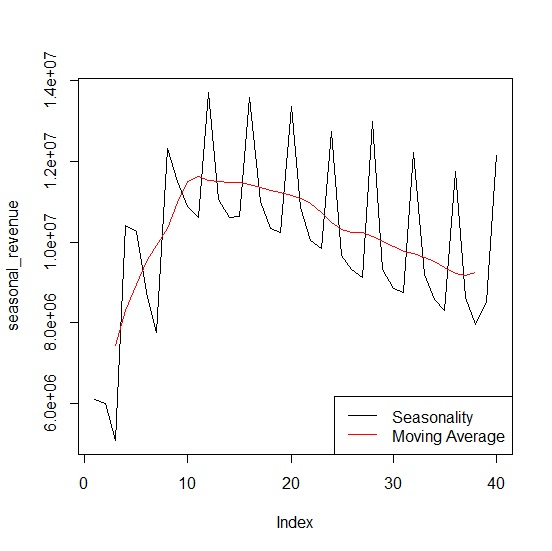
接下來只要將季營業額除以中央移動平均數,就可換算出從2011年第三季開始到2020年第二季為止的季節變動與不規則變動百分比。
> SI<-seasonal_revenue/seasonal_cma
> SI
[1] NA NA 0.6865927 1.2562995 1.1443004 0.9192676 0.7802170
[8] 1.1906145 1.0484247 0.9461463 0.9140248 1.1874968 0.9621218 0.9234138
[15] 0.9279157 1.1881235 0.9707072 0.9185933 0.9134489 1.1951625 0.9807370
[22] 0.9182302 0.9176059 1.2145374 0.9381571 0.9110314 0.8919819 1.2810604
[29] 0.9305363 0.8950763 0.8963787 1.2564168 0.9568265 0.8996595 0.8843058
[36] 1.2733166 0.9395256 0.8582074 NA NA
現在已經可以歸納出遠東百貨每年Q1到Q4營業額的季節變動與不規則變動百分比:
> SI_factor<-matrix(SI, nrow=10, ncol=4, byrow=TRUE,
+ dimnames=list(c("2011","2012","2013","2014","2015","2016","2017","2018","2019","2020"),
+ c("Q1","Q2","Q3","Q4")))
> SI_factor
Q1 Q2 Q3 Q4
2011 NA NA 0.6865927 1.256300
2012 1.1443004 0.9192676 0.7802170 1.190614
2013 1.0484247 0.9461463 0.9140248 1.187497
2014 0.9621218 0.9234138 0.9279157 1.188123
2015 0.9707072 0.9185933 0.9134489 1.195163
2016 0.9807370 0.9182302 0.9176059 1.214537
2017 0.9381571 0.9110314 0.8919819 1.281060
2018 0.9305363 0.8950763 0.8963787 1.256417
2019 0.9568265 0.8996595 0.8843058 1.273317
2020 0.9395256 0.8582074 NA NA
將每年Q1、Q2、Q3、Q4季節變動與不規則變動百分比平均,可獲得季節因子:
> SI_factor<-as.data.frame(SI_factor)
> seasonal_factor<-apply(SI_factor, 2, sum, na.rm=TRUE)/9
> seasonal_factor
Q1 Q2 Q3 Q4
0.9857041 0.9099584 0.8680524 1.2270031
季節因子加總等於3.99,但四季總和其實應該等於4,所以我們做一下校正得出季節指數:
> seasonal_index<-seasonal_factor/sum(seasonal_factor)*4
> seasonal_index
Q1 Q2 Q3 Q4
0.9879967 0.9120749 0.8700714 1.2298570
到此季節變動已經拆解完成。下面這張表格就是最後的結果。我們可以看到第四季季節指數>1表示Q4是遠東百貨的旺季,而遠東百貨的淡季則落在Q3。
> SI_factor<-rbind(SI_factor, seasonal_factor, seasonal_index)
> row.names(SI_factor)[11]<-c("s_factor")
> row.names(SI_factor)[12]<-c("s_index")
> SI_factor
Q1 Q2 Q3 Q4
2011 NA NA 0.6865927 1.256300
2012 1.1443004 0.9192676 0.7802170 1.190614
2013 1.0484247 0.9461463 0.9140248 1.187497
2014 0.9621218 0.9234138 0.9279157 1.188123
2015 0.9707072 0.9185933 0.9134489 1.195163
2016 0.9807370 0.9182302 0.9176059 1.214537
2017 0.9381571 0.9110314 0.8919819 1.281060
2018 0.9305363 0.8950763 0.8963787 1.256417
2019 0.9568265 0.8996595 0.8843058 1.273317
2020 0.9395256 0.8582074 NA NA
s_factor 0.9857041 0.9099584 0.8680524 1.227003
s_index 0.9879967 0.9120749 0.8700714 1.229857
在經營管理策略上,有時候我們想瞭解營收成長單純是來自淡旺季的影響,還是每年都能維持穩定成長,這時候排除季節變動就顯得重要。有了季節指數就完成這項工作。只要將季營業額除以季節指數,就能得出排除季節與不規則變動影響的營業額。
> seasonal_adj_revenue<-seasonal_revenue/seasonal_index
> seasonal_adj_revenue
[1] 6183716 6588493 5863003 8473122 10391139 9617959 8912063 10029803
[9] 11657638 11947103 12220286 11144422 11207500 11639373 12238952 11050164
[17] 11159255 11361019 11792486 10861148 11006591 11034750 11321963 10366042
[25] 9798405 10250170 10509162 10570065 9456217 9713621 10083663 9947135
[33] 9337944 9395595 9546160 9567058 8736116 8714519 9766334 9897115
經過季節校正後的營業額比較如下:
> plot(seasonal_revenue, type="l")
> lines(seasonal_adj_revenue, type="l", col="red")
> legend("bottomright", legend=c("Seasonal Revenue", "Seasonal Adjusted"), col=c("black", "red"), lty=1)
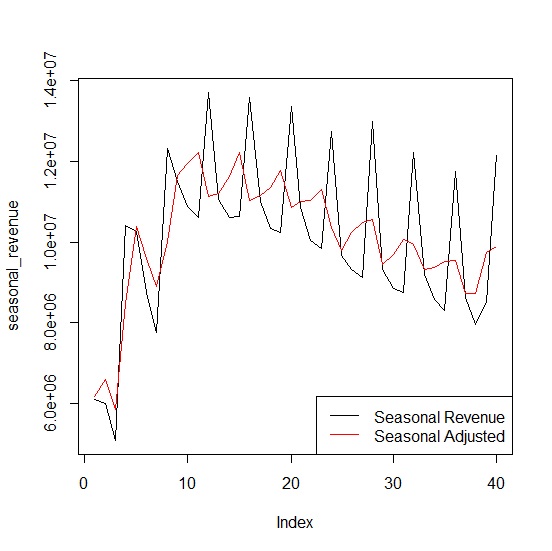
我們一樣可用迴歸分析來預測消除季節變動與不規則變動後的營業額。時間t斜率為1239,顯示遠東百貨在不考慮季節變動時,每季營業額成長1,239千元。
> revenue<-cbind(revenue, seasonal_adj_revenue)
> without_seasonal<-lm(seasonal_adj_revenue~t, data=revenue)
> without_seasonal
Call:
lm(formula = seasonal_adj_revenue ~ t, data = revenue)
Coefficients:
(Intercept) t
10008968 1239
同樣地,我們也可以建構時間序列,用R的ets()與auto.arima()模型自動預測遠東百貨未來的營業額。當然這個預測是不準確的,因為我們現在已經知道2021年受到covid-19衝擊各行各業營收下滑,這種黑天鵝事件是任何模型都無法預測的。