R統計 | 共變數分析

共變數分析是變異數分析的延伸。變異數分析比較的是兩個以上組別的差異，共變數分析也是一樣，只不過變異數分析比較的是平均數，共變數分析比較的是「調整後」的平均數。既然都是比較平均數那為什麼要做調整？

想像一下我們想瞭解不同教學方法對成績的影響，結果發現提問法的教學對學習最有幫助。不過這個結論真的是肯定的嗎？有沒有可能這群成績好的人，本來的條件就特別優異，家中可以給他/她很多資源，讓這群人的起跑點跟別人不一樣？這就是共變數分析想要討論的地方，也就是排除自身條件或家庭資源後，教學方法對成績的影響還剩下多少？

我們將這個額外多出來，卻又會影響結果的變數叫作「共變數」(covariate)。如果我們能排除共變數的影響，就更能掌握自變數對應變數的解釋力。共變數分析的原理是利用回歸模型，分別將自變數與共變數的離均差平方和(Sum of Square, SS)予以排除，再將剩下的殘差進行差異檢驗，可以看成是一種結合變異數分析與回歸分析的技巧，所以共變數必須是連續變數。其概念可以用下列示意圖來表達。

示意圖中重疊區域代表共變數與自變數對應變數的解釋力。原本共變數與自變數各有20%解釋力的時候，移除共變數後可讓自變數的解釋力提高至\(\frac{20\%}{80\%}\)=25%。不過右圖也顯示當變數交織在一起的時候，本來自變數有20%的解釋力，一旦移除共變數也等於移除自變數，自變數的整體解釋力反而只剩下\(\frac{15\%}{80\%}\)=19%。這種共變數分析所衍生的矛盾包含著名的Lord's paradox，在Miller與Chapman(2001)的論文有詳細介紹。儘管共變數分析經常和「控制」(control)某某變數連結在一起，但必須瞭解的是，共變數分析的目的是用來改善檢定力，而不是為了控制或操弄任何變數。

共變數分析與變異數分析一樣必須滿足三大前提：

獨立性：共變數與應變數應具獨立性，與自變數也應獨立，否則會衍生上述交互影響的問題。
常態性：樣本必須符合常態分配，也就是分配至少要長得差不多，奇形怪狀的分配是沒辦法比較的。
同質性：各組變異數必須相等或接近，差太多的東西無法比較。

學校教得好？還是靠爸重要？─ANOVA模型

延續上面的例子，到底成績好是因為學校教得好？還是家裡比較有錢可以栽培？我們以teaching.csv為例進行說明，這是一個虛擬出來的資料檔。首先載入資料並將教學方法由原本的數值改為提問法、發現法、小組討論以及填鴨法四種類別變數。


     > teaching<-read.csv("c:/Users/USER/Downloads/teaching.csv", header=T, sep=",")
     
     > method<-factor(teaching$method, levels=c(1,2,3,4), labels=c("question","discovery","discussion","spoonfeeding"))

     > teaching<-teaching[,-c(3)]

     > teaching<-cbind(teaching, method)

     > str(teaching)

     'data.frame':   36 obs. of  3 variables     
      $ score : int  90 74 26 100 70 80 66 34 24 78 ...
      $ income: int  106 69 71 117 106 127 75 52 26 157 ...
      $ method: Factor w/ 4 levels "question","discovery",..: 1 1 1 1 1 1 1 1 2 2 ...
     > rm(method)

     > attach(teaching)

資料中包含36筆觀察值，分別記錄學習成績、父親年收入以及四種不同教學方法。箱型圖顯示四種方法中，提問法的教學法成績比較好，最差的是填鴨式教育。


     > tapply(score, method, mean)

         question    discovery   discussion spoonfeeding
            67.50        45.75        43.80        31.60
     > boxplot(score~method)

變異數分析得知，這樣的成績差異是有統計意義的。


     > summary(aov(score~method, data=teaching))

                 Df Sum Sq Mean Sq F value  Pr(>F)
     method       3   5820  1940.0   4.503 0.00958 **
     Residuals   32  13787   430.9
     ---
     Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1*

接著我們要問，這樣的差異會不會來自於家庭資源？如果排除家庭資源的影響，不同的教學方法對成績的影響又是如何？因此我們納入父親年收入這項共變數。

前置作業：三大前提檢定

共變數分析前應先確定三大前提：獨立性、常態性與同質性。我們先檢定獨立性。獨立性假設各類分組中的共變數與應變數互相獨立，也就是散布圖中的回歸線斜率應平行。我們先將資料依教學法分組分別計算其回歸線。


     > library(dplyr)

     > question<-filter(teaching, method=="question")

     > discovery<-filter(teaching, method=="discovery")

     > discussion<-filter(teaching, method=="discussion")

     > spoonfeeding<-filter(teaching, method=="spoonfeeding")

     > plot(income, score, col=method)

     > abline(lm(question$score~question$income, data=question))

     > abline(lm(discovery$score~discovery$income, data=discovery), col="red")

     > abline(lm(discussion$score~discussion$income, data=discussion), col="dodgerblue")

     > abline(lm(spoonfeeding$score~spoonfeeding$income, data=spoonfeeding), col="green")

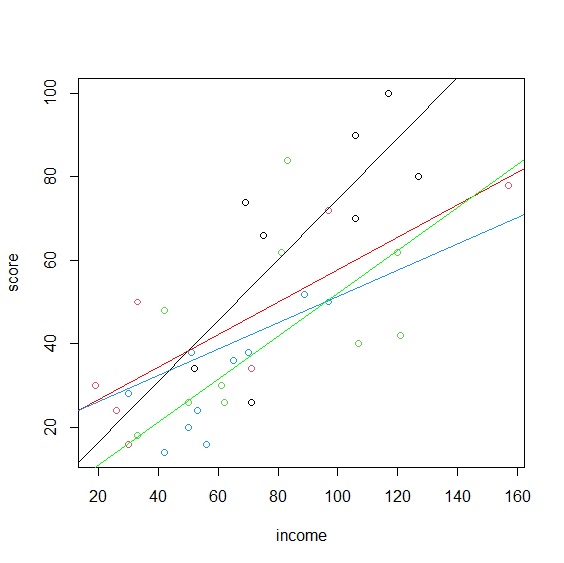
散布圖中的四條回歸線沒有完全平行，嚴格來說不符合共變數分析的假設條件，但斜率已經很接近。接下來以shapiro.test()檢定常態分配。四種教學方法都>.05符合常態分配假設。


     > teaching %>%

     + group_by(method) %>%

     + summarize(p_value=shapiro.test(income)$p.value)

     # A tibble: 4 x 2
       method       p_value
       <fct>          <dbl>
     1 question       0.447
     2 discovery      0.201
     3 discussion     0.417
     4 spoonfeeding   0.635

最後bartlett.test()檢定結果>.05，符合變異數同質性假設。


     > bartlett.test(income~method, data=teaching)

     

             Bartlett test of homogeneity of variances
     

     data:  income by method
     Bartlett's K-squared = 6.8268, df = 3, p-value = 0.07763

共變數分析

確定符合分析的前提假設後，直接用aov()進行共變數分析。指令與變異數分析一樣，只要在自變數後面加上共變數即可。


     > ancova<-aov(score~method+income, data=teaching)

     > summary(ancova)

                 Df Sum Sq Mean Sq F value   Pr(>F)
     method       3   5820    1940   8.508 0.000286 ***
     income       1   6719    6719  29.466 6.29e-06 ***
     Residuals   31   7069     228
     ---
     Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

值得一提的是，這裡必須注意離均差平方和(Sum of Squares, SS)有Type I、Type II、Type III三種型態。aov()預設是Type I適用於均衡性資料(balanced data)，Type II與Type III適用於不均衡資料(unbalanced data)。關於三種類型的差異多倫多大學統計系的Nancy Reid有詳細介紹。一般來說不知道如何選擇的時候，Type III是應用比較廣泛的選擇。事實上如果多加注意的話，ancova報表最後一行就有這段文字：Estimated effects may be unbalanced，R已經提醒資料不均衡。


     > ancova

     Call:
        aov(formula = score ~ method + income, data = teaching)
     

     Terms:
                       method   income Residuals
     Sum of Squares  5820.056 6718.812  7068.688
     Deg. of Freedom        3        1        31
     

     Sum of Squares  5820.056 6718.812  7068.688
     Estimated effects may be unbalanced

所以本例中我們要改為Type III的離均差平方和。這項工作可由car套件中的Anova()來完成。分析結果可以發現無論Type I或Type III，教學方法與父親年收入對成績都有顯著影響，可見父親年收入這項共變數也對成績高低有部分解釋力，這就是共變數分析想要調整的部分。


     > library(car)

     > Anova(ancova, type="III")

     Anova Table (Type III tests)
     

     Response: score
                 Sum Sq Df F value   Pr(>F)
     (Intercept) 2337.6  1 10.2516  0.00315 **
     method      2296.7  3  3.3574  0.03125 *
     income      6718.8  1 29.4656 6.29e-06 ***
     Residuals   7068.7 31
     ---
     Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

控制父親年收入這項共變數後，四種教學方法到底對成績有什麼影響？我們可以用emmeans套件中的emmeans()或lsmeans()兩個指令來計算調整後的邊際平均。


     > library(emmeans)

     > emmeans(ancova, "method")

      method       emmean   SE df lower.CL upper.CL
      question       60.2 5.51 31     48.9     71.4
      discovery      47.5 5.35 31     36.6     58.5
      discussion     42.6 4.78 31     32.9     52.4
      spoonfeeding   37.2 4.89 31     27.2     47.2
     

     Confidence level used: 0.95

分析結果

上述emmean平均數就是控制共變數的「調整後」平均數。比較調整前與調整後的差異可以發現，原本提問法的成績經過調整後大幅下降，而填鴨教育的成績則顯著上升，表示在控制父親年收入這項共變數後，不同教學法的成績差異就沒那麼明顯了。可見無論教學方法如何改變，家庭資源都還是對成績有明顯影響。

	調整前	調整後
提問法	67.5	60.2
發現法	45.8	47.5
討論法	43.8	42.6
填鴨法	31.6	37.2

學校教得好？還是靠爸重要？─回歸模型

共變數分析被歸類在一般線性模式(General Linear Model, GLM)中，是一種混合變異數分析與回歸分析的方法。其實如果從回歸分析著手，更能體會為什麼共變數分析會被歸類在一般線性模型，因為其實它就是一種虛變數回歸。

為了證明共變數分析其實就是虛變數回歸分析，我們將原本的類別資料教學法，先用dummy.code()設定為虛變數。


     > library(psych)

     > method_dummy<-dummy.code(teaching$method)

     > teaching<-cbind(teaching, method_dummy)

     > head(teaching)

       score income   method discussion spoonfeeding question discovery
     1    90    106 question          0            0        1         0
     2    74     69 question          0            0        1         0
     3    26     71 question          0            0        1         0
     4   100    117 question          0            0        1         0
     5    70    106 question          0            0        1         0
     6    80    127 question          0            0        1         0

虛變數設定後原資料合併，可以看到原本teaching資料集增加代表每一種教學法的四個虛變數欄位。我們現在以填鴨法為參考基準進行虛變數回歸。


     > ancova_glm<-lm(score~question+discovery+discussion+spoonfeeding+income, data=teaching)

     > summary(ancova_glm)

     

     Call:
     lm(formula = score ~ question + discovery + discussion + spoonfeeding +
         income, data = teaching)
     

     Residuals:
         Min      1Q  Median      3Q     Max
     -33.162  -7.940  -3.226   9.680  37.188
     

     Coefficients: (1 not defined because of singularities)
                  Estimate Std. Error t value Pr(>|t|)
     (Intercept)   5.65075    6.75683   0.836  0.40939
     question     22.95765    7.54915   3.041  0.00476 **
     discovery    10.35229    7.19684   1.438  0.16033
     discussion    5.44373    6.86685   0.793  0.43395
     spoonfeeding       NA         NA      NA       NA
     income        0.43034    0.07928   5.428 6.29e-06 ***
     ---
     Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
     

     Residual standard error: 15.1 on 31 degrees of freedom
     Multiple R-squared:  0.6395,    Adjusted R-squared:  0.593
     F-statistic: 13.75 on 4 and 31 DF,  p-value: 1.479e-06

我們的虛變數回歸模型根據上述分析結果為：

\[y=5.6508+22.9577_{question}+10.3523_{discovery}+5.4437_{discussion}+0.4303_{income}\]

回歸模型已將父親年收入納入考量，因此我們可以據此計算調整後的平均數。所有觀察值年收入平均為73.31萬元，將數字代入回歸模型得出最後結果：

\(\text{提問法： }5.6508+22.9577 \times 1 + 10.3523 \times 0 + 5.4437 \times 0 + 0.4303 \times 73.31 = 60.2\)

\(\text{發現法： }5.6508+22.9577 \times 0 + 10.3523 \times 1 + 5.4437 \times 0 + 0.4303 \times 73.31 = 47.5\)

\(\text{討論法： }5.6508+22.9577 \times 0 + 10.3523 \times 0 + 5.4437 \times 1 + 0.4303 \times 73.31 = 42.6\)

\(\text{填鴨法： }5.6508+22.9577 \times 0 + 10.3523 \times 0 + 5.4437 \times 0 + 0.4303 \times 73.31 = 37.2\)

另一個計算調整後平均數的方法是利用下列公式：

\[y'_{j}=y_{j}-B(x_{j}-\bar{x})\]

在這個公式中B是共變數的回歸斜率0.43034，\(x_{j}-\bar{x}\)是共變數在四種教學法的離均差，\(y_{j}\)是自變數在四種教學法的平均數。計算如下：


     > tapply(score, method, mean)

         question    discovery   discussion spoonfeeding
            67.50        45.75        43.80        31.60
     > tapply(income, method, mean)

         question    discovery   discussion spoonfeeding
           90.375       69.125       76.000       60.300
     > mean(score)

     [1] 46.11111
     > mean(income)

     [1] 73.30556

根據上述計算結果可以整理如下表。無論是採用哪一種方法，所獲得結論都是相同的。

	y (score)	x (income)	y' (adj)
提問法	67.50	90.375	\(67.50-0.43034\times(90.375-73.30556)=60.2\)
發現法	45.75	69.125	\(45.75-0.43034\times(69.125-73.30556)=47.5\)
討論法	43.80	76.000	\(43.80-0.43034\times(76.000-73.30556)=42.6\)
填鴨法	31.60	60.300	\(31.60-0.43034\times(60.300-73.30556)=37.2\)
總平均	46.11111	73.30556

簡介

學校教得好？還是靠爸重要？─ANOVA模型

前置作業：三大前提檢定

共變數分析

分析結果

學校教得好？還是靠爸重要？─回歸模型