特徵有很多種,但有沒有一個最重要的特徵,可以說明這件人、事、物的本質?化簡馭繁,一直是數學的目的,也是一百多年前卡爾·皮爾森(Karl Pearson)發明主成分分析(Principal Component Analysis, PCA)的緣由。
主成分分析是一個降低維度的方法,因為維度太多雖然可以精確描述特徵,但卻也造成「維度詛咒」(curse of dimensionality)。用白話來說就是「太複雜」。所以我們希望把事情簡單化,只要用一兩個最具代表的特徵來描述就好。
數學上為了要把一堆特徵化簡,需要用到向量(vector)、正射影(orthographic projection)等概念,並用正交矩陣(orthogonal matrix)對資料進行線性轉換,從而找出線性不相關、彼此變異最大的變數,也就是變異數越大越好的線性組合。所以主成分分析其實就是在分析共變異數矩陣(covariance matrix),矩陣的特徵向量(eigenvector)就是主成分,特徵值(eigenvalue)由大到小依序排列就是第一主成分、第二主成分...。
主成分分析的計算涉及一系列線性代數,看起來相當複雜。其實我們日常生活中就會碰到類似主成分分析的情況。舉例來說,在決定要不要共度一輩子的時候,考慮的因素很多,包含對自己好不好、個性善不善良、與父母相處、有沒有車、有沒有房、存款有多少等等。有時候考慮因素太多,反而很難作出決定。這時候通常會回到原點,思考對方到底愛不愛自己,或你自己愛不愛她/他?因為愛不愛可以解釋他對你好不好、願不願意花錢在你身上、你願不願意容忍跟他相處等因素。這就是主成分分析,我們從眾多考慮中萃取出最重要的因素「愛不愛」。
又例如買車,我們可能會考慮一台車的廠牌、型式、馬力、空間、外觀、進口或國產、用途等等,去了很多展示中心,也是試乘不同車款,最後作決定的可能是「預算」。因為預算涵蓋了廠牌、型式、馬力等前面羅列的因素,那麼「預算」就是購車最重要的主成分。
主成分分析與因素分析(Factor Analysis)是兩種不同的方法,但目的都是減少變數數量。主成份分析是找出變異最大的特徵,使得樣本在這些特徵上呈現最大差異;而因素分析更關注這些特徵的線性模型。兩者都是線性降維的資料簡化技巧,不少統計軟體甚至教科書都將因素分析視為主成份分析的特殊情形,本部分以介紹主成份分析為主。主成分分析要先計算共變異數:
\[cov(X,Y)=\frac{\displaystyle\sum_{i=1}^{N}(x_{i}-\overline{x})(y_{i}-\overline{y})}{N-1}\]
第一個主成分到第n個主成分,可以透過下列公式來表示。其中\(\phi\)是每一個主成分的特徵向量。
\[PC_{1}=\phi x_{1}+\phi x_{2}+\dots+\phi x_{n}\]
\[PC_{2}=\phi x_{1}+\phi x_{2}+\dots+\phi x_{n}\]
\[\vdots\]
\[PC_{n}=\phi x_{1}+\phi x_{2}+\dots+\phi x_{n}\]
三國志14最重要的能力是什麼?
三國志14(Romance of the Three Kingdoms XIV)是一款由日本遊戲公司以三國歷史為背景所開發的一款遊戲。從1985年第一代開始到現在已經發行14代,是一款廣受歡迎的戰略遊戲。三國志登場的人物超過千人,人物含有統率、武力、智力、政治、魅力等能力值,也就是俗稱的五維。我們分別從魏蜀吳中各挑選10位名將作為樣本,並針對五維進行主成分分析。
由於三國名將眾多無法一一挑選,所以曹魏的部分我們挑選曹操、張遼、徐晃、于禁、樂進、張郃、荀彧、程昱、郭嘉、司馬懿;孫吳我們挑選孫權、周瑜、魯肅、呂蒙、陸遜、甘寧、太史慈、黃蓋、程普、周泰;蜀漢則挑選劉備、關羽、張飛、馬超、黃忠、趙雲、諸葛亮、龐統、法正、姜維。這些這30人已經包含五子良將、五虎上將以及知名謀臣。五維的數據則來自網路,整理後的資料threekingdoms.csv可直接下載。首先載入資料:
> threekingdoms<-read.csv("c:/Users/USER/Downloads/threekingdoms.csv", header=T, sep=",")
> head(threekingdoms)
角色 國家 統率 武力 智力 政治 魅力
1 曹操 魏 98 72 91 94 96
2 張遼 魏 95 92 78 58 77
3 徐晃 魏 88 90 74 48 73
4 于禁 魏 84 77 72 57 56
5 樂進 魏 80 84 53 51 65
6 張郃 魏 89 89 69 57 72
> threekingdoms<-data.frame(threekingdoms, row.names=threekingdoms$角色) #將資料集的列編碼改為角色名稱
> threekingdoms<-threekingdoms[,-c(1)] #刪除資料集原有的角色名稱
> head(threekingdoms)
國家 統率 武力 智力 政治 魅力
曹操 魏 98 72 91 94 96
張遼 魏 95 92 78 58 77
徐晃 魏 88 90 74 48 73
于禁 魏 84 77 72 57 56
樂進 魏 80 84 53 51 65
張郃 魏 89 89 69 57 72
> attach(threekingdoms)
資料整理完畢後,可以開始進行主成分分析。R分別有prcomp()、princomp()兩個指令可以進行主成分析,兩個指令輸出的內容大同小異,下表顯示兩者的指令差別。這裡我們先用prcomp()來進行分析。
| prcomp() | princomp() | 說明 |
|---|---|---|
| sdev() | sdev() | 主成分的標準差,標準差平方為特徵值 |
| rotation() | loadings() | 主成分的特徵向量 |
| x() | scores() | 觀察值位於座標上的向量,也就是主成分分數 |
主成分分析
雖然三國志14中的能力值數據採用相同的單位,但還是要保持將資料標準化的習慣。所以記得設定center=TRUE, scale=TRUE參數。
> pca_threekingdoms<-prcomp(~統率+武力+智力+政治+魅力, data=threekingdoms, center=TRUE, scale=TRUE)
> pca_threekingdoms
Standard deviations (1, .., p=5):
[1] 1.7003846 1.1817577 0.7205458 0.3261005 0.2943009
Rotation (n x k) = (5 x 5):
PC1 PC2 PC3 PC4 PC5
統率 -0.1780333 -0.7459706 -0.465391990 0.3066129 -0.3181679
武力 -0.4988823 -0.3945047 0.149520489 -0.3022959 0.6940773
智力 0.5246649 -0.1367890 -0.499880820 -0.6650997 0.1173755
政治 0.5606584 -0.1386170 -0.006379638 0.5774180 0.5770575
魅力 0.3602908 -0.4999680 0.714935231 -0.1970699 -0.2650540
> pca_threekingdoms$sdev^2 #計算特徵值,每個主成分的標準差平方
[1] 2.89130786 1.39655131 0.51918628 0.10634152 0.08661303
我們可以將30位角色根據能力值分別正射影到5個主成分上,並計算各角色的新向量,也就是主成分分數(principal component scores)。
> head(pca_threekingdoms$x)
PC1 PC2 PC3 PC4 PC5
曹操 1.2621074 -1.7849878 -0.1008980 0.35485596 0.014959057
張遼 -0.8589525 -0.9322761 -0.3764937 -0.16743469 0.005426583
徐晃 -1.1668501 -0.1709173 -0.1523745 -0.40077128 -0.052887536
于禁 -1.0763405 0.8615060 -0.8203034 0.18036043 0.216977450
樂進 -1.6569033 0.9150900 0.3820584 0.42464583 0.096981503
張郃 -1.1118499 -0.2088852 -0.1106571 0.07796388 0.104661300
上面就是主成份分析的結果。5個主成分中每個能力值各有其特徵向量。因為向量同時具有方向與大小,所以也可以看成每個能力值對每個主成分的負荷量。第1主成分PC1的政治、智力、魅力特徵向量為正;第2主成分PC2的特徵向量則都是負;第3成分PC3特徵向量為正的有魅力跟武力;第4成分PC4特徵向量正向有政治與統率、最後第5成分PC5正向的則有武力、政治、智力。負荷圖可以更清楚呈現每個能力值在5個主成分中的負荷量。
> par(mfrow=c(1,5)) #設定圖表輸出版型為1x5
> sorted_loading<-load[order(load[,1]),1] #第1主成分負荷量排序
> dotchart(sorted_loading, main="Loading Plot for PC1", xlab="Variable Loading", pch=16, col="red") #輸出第1主成分負荷圖
> sorted_loading<-load[order(load[,2]),2] #第2主成分負荷量排序
> dotchart(sorted_loading, main="Loading Plot for PC2", xlab="Variable Loading", pch=16, col="blue") #輸出第2主成分負荷圖
> sorted_loading<-load[order(load[,3]),3] #第3主成分負荷量排序
> dotchart(sorted_loading, main="Loading Plot for PC3", xlab="Variable Loading", pch=16, col="purple") #輸出第3主成分負荷圖
> sorted_loading<-load[order(load[,4]),4] #第4主成分負荷量排序
> dotchart(sorted_loading, main="Loading Plot for PC4", xlab="Variable Loading", pch=16, col="darkgreen") #輸出第4主成分負荷圖
> sorted_loading<-load[order(load[,5]),5] #第5主成分負荷量排序
> dotchart(sorted_loading, main="Loading Plot for PC5", xlab="Variable Loading", pch=16, col="black") #輸出第5主成分負荷圖
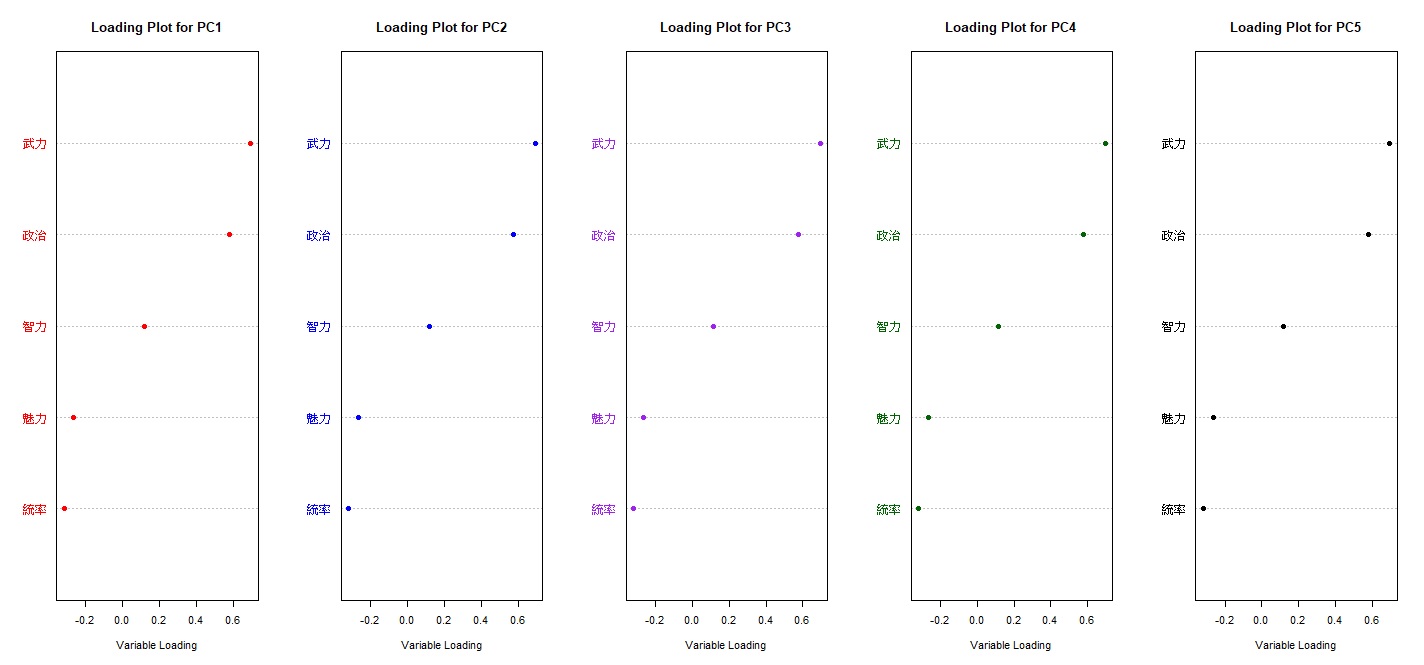
那麼到底這五個能力值萃取出最重要的成分(特徵)是什麼?我們可以藉由summary()或plot()及factoextra套件裡的fviz_eig()指令繪製陡坡圖來判斷。
> summary(pca_threekingdoms)
Importance of components:
PC1 PC2 PC3 PC4 PC5
Standard deviation 1.7004 1.1818 0.7205 0.32610 0.29430
Proportion of Variance 0.5783 0.2793 0.1038 0.02127 0.01732
Cumulative Proportion 0.5783 0.8576 0.9614 0.98268 1.00000
> library(factoextra)
> plot(pca_threekingdoms, type="line", main="Scree Plot")
> fviz_eig(pca_threekingdoms)
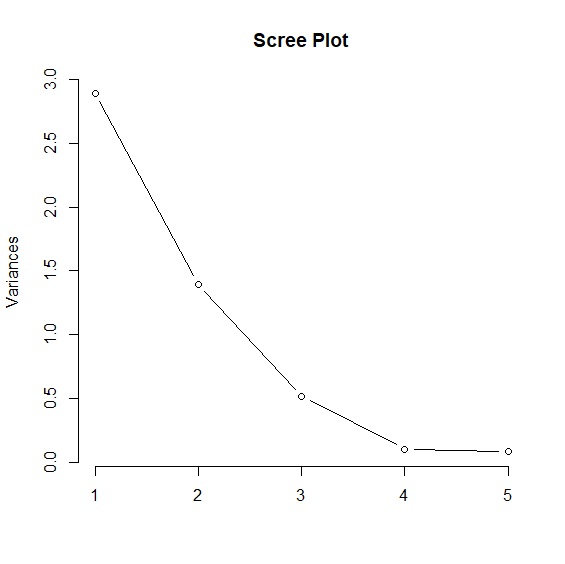
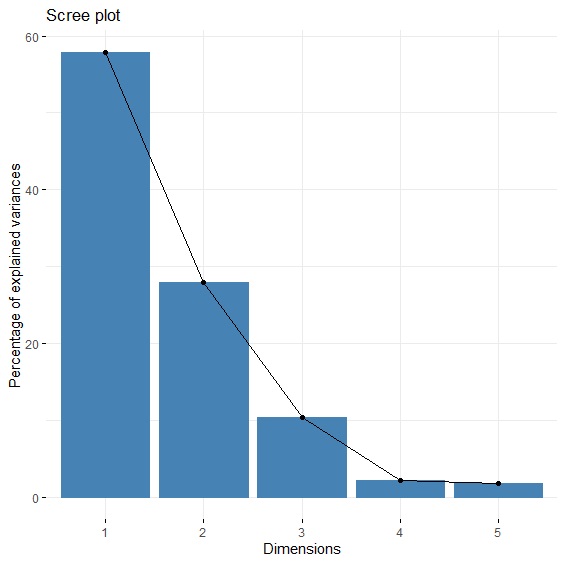
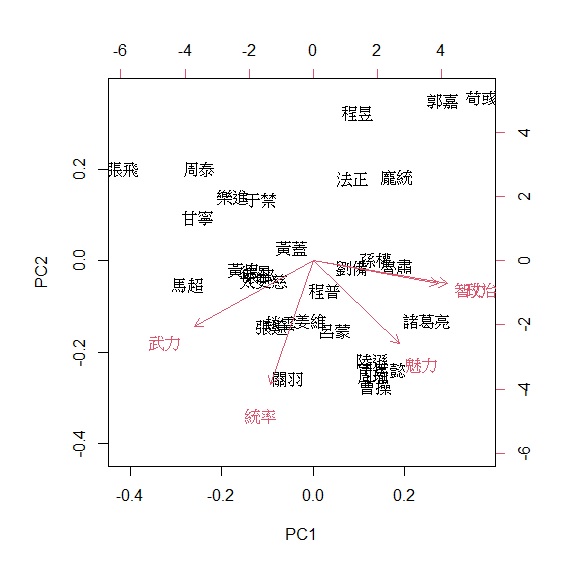
summary()報告5個主成分中,每個成分可解釋的變異以及累積變異量。由於第1主成分PC1已經可解釋統率+武力+智力+政治+魅力五個能力值57.83%的變異,第2主成分可解釋27.93%,兩個主成分已經可以涵蓋85.76%的變異量。所以我們就最終只需考慮第1主成分PC1與第2主成分PC2。原本的五個能力值,經過主成分分析降維後,縮減為剩下兩個維度,並據此畫出30位角色在兩個維度上的位置。
圖中根據兩個主成分畫分為四個象限,並顯示出五個能力值的向量,其中智力與政治的向量幾乎重疊。第1主成分(y軸)的右半邊是角色的運籌帷幄能力,所以多半都是君主與謀士;左半邊是角色帶兵打仗的能力,所以多半都是名將。五個能力的正向量都集中在第2主成分(x軸)下半部,上半部是負向量,所以第一象限是屬於缺少實際帶兵打仗的謀士,第二象限偏向缺乏謀略的將軍。所以根據分析,我們可將第1主成分命名為「文臣武將」、第2主成分命名為「智勇雙全」。
這樣的分析結果其實不難理解,甚至可以不用分析就能猜測結果。因為整個三國志中角色最大的區別就是謀士與武將。統率、武力、智力、政治、魅力五種能力中,統率、武力本來就是武將屬性,後面三種能力本來就是君主謀士的能力值。無怪乎第1主成分就有近六成的解釋變異量。
預測新角色
主成分分析的結果,是賦予每個觀察值新的向量座標。如果有新的觀察值,我們也可以據此判斷這些觀察值在主成分上的座標位置。這裡已經事先準備好new_character.RData,裡頭包含曹丕、賈詡、荀攸、孫堅、張昭、韓當、魏延、馬謖、黃權九人,我們可以據此計算他們的座標,同時用fviz_add()把這九人在座標象限上標示出來。
> load(file="c:/Users/USER/downloads/new_character.RData")
> new_character
國家 統率 武力 智力 政治 魅力
曹丕 魏 70 71 83 86 84
賈詡 魏 86 48 97 85 57
荀攸 魏 73 26 94 88 86
孫堅 吳 94 90 77 72 90
張昭 吳 33 3 84 97 81
韓當 吳 76 85 59 51 68
魏延 蜀 84 92 69 46 39
馬謖 蜀 64 67 87 68 67
黃權 蜀 76 59 85 79 80
> pca_predict<-predict(pca_threekingdoms, newdata=new_character)
PC1 PC2 PC3 PC4 PC5
曹丕 1.0269272 0.7491800 0.7936185 -0.19706442 0.7933031
賈詡 0.9709983 0.7907356 -1.7661751 0.36120158 0.1930792
荀攸 2.3392870 1.1070209 0.1606568 0.06241825 -0.5071835
孫堅 -0.1628053 -1.3456934 0.3074686 0.05574542 0.1008312
張昭 3.3021889 4.5334725 1.8434139 -0.14236276 0.3025507
韓當 -1.3559942 1.0361889 0.5393102 0.02587952 0.2344672
魏延 -2.1674195 1.2807628 -1.4580198 0.04771733 0.6494948
馬謖 0.4671785 1.8974219 0.1065313 -0.71506234 0.7263342
黃權 0.9607196 0.6801303 0.2032522 -0.07414849 0.1681056
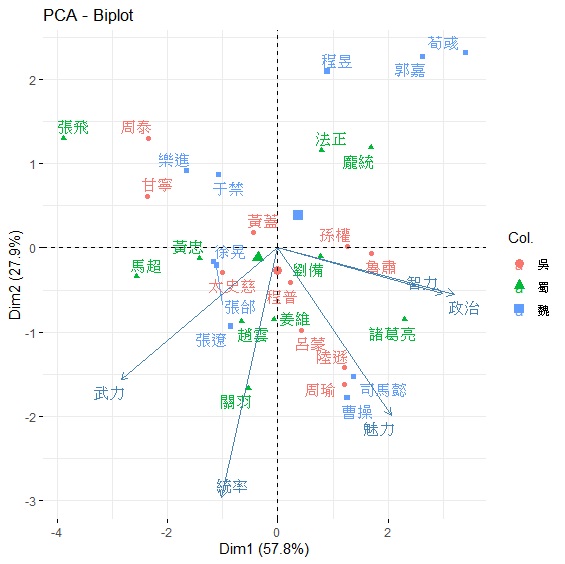
> biplot<-fviz_pca_biplot(pca_threekingdoms, col.ind=國家, repel=TRUE)
> fviz_add(biplot, pca_predict, color="black", repel=TRUE)

整體而言,在三國志14的設定中,透過主成分分析第一象限包含知名的謀士,第二象限則是有名的武將,第三象限的武將除了有名之外,還特別hightlight出領導統御的表現,例如關羽威震華夏、張遼威震逍遙津、黃忠有定軍山之役、馬超有潼關之役、太史慈北海救孔融、趙子龍單騎救主都加強了遊戲中武力與統率的設定,第四象限則是以領導人為主。
MVP最重要的條件是什麼?
NBA每個球季票選一名最有價值球員,票選制度最早是球員互相投票,後來改為媒體共同投票,2010年開始其中一張選票也加入了球迷網路投票。MVP被視為該球季最出色的球員,不僅是球技的肯定,更是賽場上統治力的表現。回顧歷史,幾乎所有拿過MVP的球員都會入選名人堂。目前Kareem Abdul-Jabbar是獲獎次數最多的球員,共有六次;其次是Bill Russel與Michael Jordan共有五次。
不過由於是票選,所以每年都難免有遺珠之憾,甚至是爭議。近年最有名的爭議來自2008年的Kobe Bryant vs. Chris Paul。那年CP3是助攻王+抄截王,同時Win Share高居聯盟第一,KB8只排第五。CP3幾乎所有進階數據都全面獲勝,同時帶領New Orleans Hornets打出了56-26的戰績,而Los Angeles Lakers的戰績是57-25,只多出一勝。最終Kobe Bryant獲得了他生涯唯一一座MVP,不少人認為因為那年Kobe Bryant已經30歲生涯即將走下坡,如果再無MVP肯定可能終生無緣,所以才獲得了關鍵票數。
遠一點的還有1997年 Michael Jordan vs. Karl Malone。這年MJ場均29.6分、5.9籃板、4.3助功,率領Chicago Bulls拿下69-13聯盟第一戰績,但最後聯盟卻將MVP頒給了場均27.4、9.9、4.5的Karl Malone,且Utah Jazz雖為西區第一,但戰績只有64-18。Malone各項數據明顯不如MJ,這也導致兩隊在總冠軍戰第一戰碰頭,Malone讀秒階段錯失兩罰後,MJ投進絕殺,被媒體與球迷拿來大做文章。不少人認為因為MJ長期統治聯盟,大家已經審美疲勞,才讓本來該屬於MJ的第六座MVP,頒給了Karl Malone。
所以MVP的特徵到底是什麼?是球隊戰績?還是個人表現?我們可以從過去獲得MVP的得主,用主成分分析歸納出這些球員的特徵,試著看看MVP的「成分」到底是什麼?我們整理出mvp.RData,包含1980年到2020年所有獲得MVP球員的基本攻守數據,同時計算當季的球隊勝率,載入如下:
> load("c:/Users/USER/Downloads/mvp.RData")
> WR<-round(mvp$W/mvp$G,2)
> mvp<-cbind(mvp, WR)
> head(mvp)
Tm P Age G W MP PTS TRB AST STL BLK FG. X3P. FT. WS WS.48 WR
20 Jokic DEN C 25 72 47 34.6 26.4 10.8 8.3 1.3 0.7 0.566 0.388 0.868 15.6 0.301 0.65
19 Antetokounmpo MIL PF 25 63 56 30.4 29.5 13.6 5.6 1.0 1.0 0.553 0.304 0.633 11.1 0.279 0.89
18 Antetokounmpo MIL PF 24 72 60 32.8 27.7 12.5 5.9 1.3 1.5 0.578 0.256 0.729 14.4 0.292 0.83
17 Harden HOU SG 28 72 65 35.4 30.4 5.4 8.8 1.8 0.7 0.449 0.367 0.858 15.4 0.289 0.90
16 Westbrook OKC PG 28 81 47 34.6 31.6 10.7 10.4 1.6 0.4 0.425 0.343 0.845 13.1 0.224 0.58
15 Curry GSW PG 27 79 73 34.2 30.1 5.4 6.7 2.1 0.2 0.504 0.454 0.908 17.9 0.318 0.92
我們將挑選年齡、得分、籃板、助攻、抄截、火鍋、Win Share以及球隊勝率八項指標進行主成分分析,分析之前要將數據標準化,避免受到單位影響。
> mvp[,c("Age","PTS","TRB","AST","STL","BLK","WS","WR")]<-scale(
+ mvp[,c("Age","PTS","TRB","AST","STL","BLK","WS","WR")])
接下來我們用另一個R的指令princomp()來萃取主成分。princomp()可以透過cor=TRUE來標準化變數,因為我們已經完成標準化,所以可以設定cor=FALSE。
> pca_mvp<-princomp(formula=~Age+PTS+TRB+AST+STL+BLK+WS+WR, data=mvp, cor=FALSE, scores=TRUE)
> pca_mvp
Call:
princomp(formula = ~Age + PTS + TRB + AST + STL + BLK + WS +
WR, data = mvp, cor = FALSE, scores = TRUE)
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
1.5425879 1.3812191 1.0187069 0.9784529 0.7928839 0.6242334 0.5592807
Comp.8
0.4373484
8 variables and 41 observations.
> summary(pca_mvp)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 1.5425879 1.3812191 1.0187069 0.9784529 0.79288390
Proportion of Variance 0.3048834 0.2444326 0.1329635 0.1226630 0.08054769
Cumulative Proportion 0.3048834 0.5493159 0.6822794 0.8049424 0.88549010
Comp.6 Comp.7 Comp.8
Standard deviation 0.62423339 0.55928069 0.43734836
Proportion of Variance 0.04992613 0.04007685 0.02450693
Cumulative Proportion 0.93541623 0.97549307 1.00000000
上面的報表顯示每一個主成分的標準差,由於標準差平方就是特徵值,所以可以直接看到依據特徵值大小排序後的8個主成分,其中第1個主成分能解釋30.5%的變異、第2主成分能解釋24.4%的變異,累計可解釋變異量約55%。接著可以呼叫scores,顯示每個球員投影在主成分上的新向量。
> head(pca_mvp$scores)
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
20 Jokic -0.1562165 0.29497127 -2.00051198 0.3804174 0.09343047
19 Antetokounmpo -0.8357851 1.14592329 -0.06918274 -1.2844182 -2.19008380
18 Antetokounmpo -1.0666296 0.38531657 -0.57066140 -1.1822546 -0.90237656
17 Harden 1.3820543 -0.82578855 0.70234423 -0.8903153 -0.57015376
16 Westbrook 0.4077638 -0.05521598 -2.07383120 2.0449538 -0.46963888
15 Curry 1.2739010 -1.67881001 1.04810851 -1.2173300 -0.52660773
Comp.6 Comp.7 Comp.8
20 Jokic 0.47747420 0.23102993 -0.381356197
19 Antetokounmpo 0.16274566 1.05124769 0.264943325
18 Antetokounmpo -0.27814295 0.61661937 -0.079712978
17 Harden 0.05902182 0.41629343 1.015706559
16 Westbrook 0.92060204 1.17040082 0.598475945
15 Curry 0.23924353 0.02731401 0.0024492093
輸出每個變數的特徵向量,並繪製第1主成分與第2主成分雙標圖。
> components<-get_pca_var(pca_mvp)
> components$contrib
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8
Age 2.115964 6.18922658 43.92061696 26.93763990 8.808760985 6.6269513 1.61835772 3.7824828
PTS 4.879376 32.23839119 0.03795471 1.92349947 18.269098220 12.6151568 3.45512258 26.5814014
TRB 28.495381 5.40756410 0.16399277 0.04502568 0.083549192 4.0199243 47.62653919 14.1580240
AST 24.428409 0.19269571 16.30449098 2.17139080 12.606167403 0.2546374 29.76140350 14.2808051
STL 4.562688 30.24536702 3.18108303 8.35789720 0.002168799 30.2217562 11.85514671 11.5738935
BLK 30.243994 0.31412874 0.27426051 0.13680720 11.135988834 32.7737390 0.01247202 25.1086100
WS 3.017826 25.40170726 0.56095926 6.62844298 45.379204736 12.8441528 2.29021429 3.8774923
WR 2.256363 0.01091941 35.55664179 53.79929676 3.715061832 0.6436820 3.38074398 0.6372909
> fviz_pca_biplot(pca_mvp, col.ind=mvp$P, repel=TRUE)
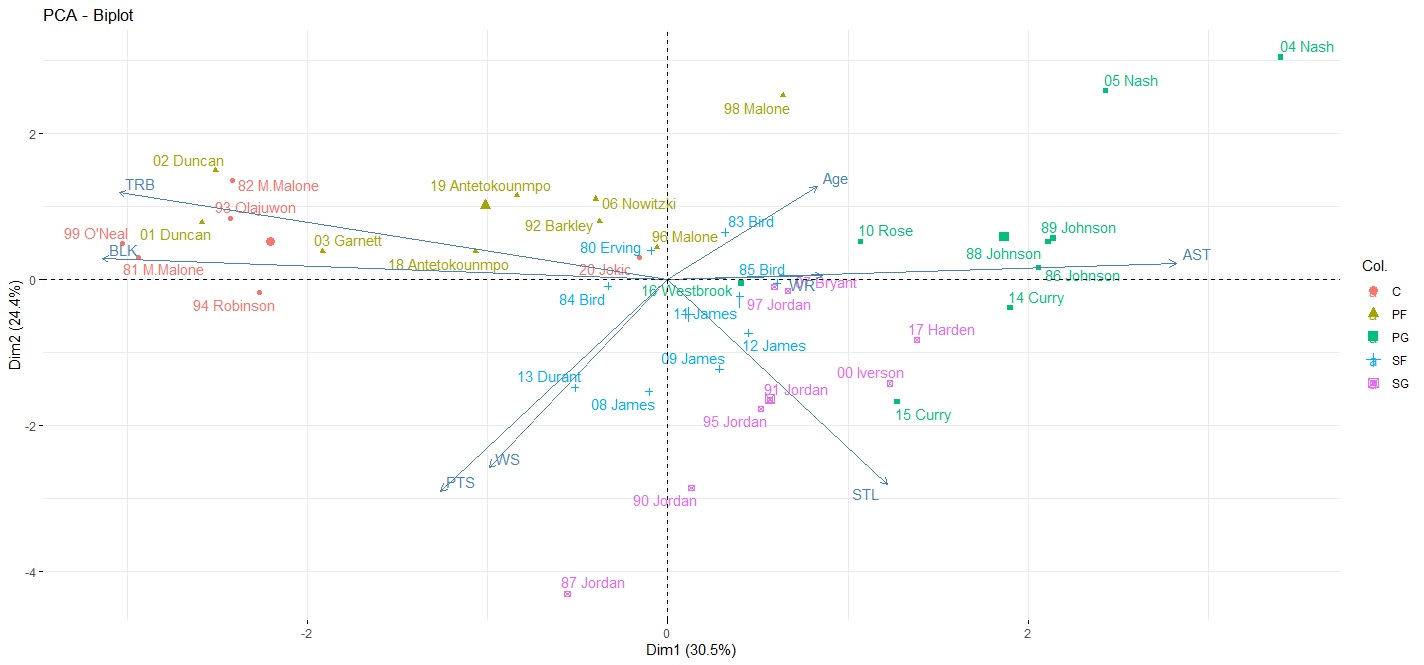
圖中可以看到每個球員在向量座標上的位置。在第1主成分(y軸)左半邊是偏向得分、Win Share、籃板、火鍋;右半邊則是助攻、抄截、年齡、勝率。其中勝率的向量是是八個主成分當中最小的,可見勝率並不是MVP的充分條件。而第2主成分(x軸)的上方則是籃板、火鍋、助攻,下方是得分、抄截、Win Share。
由此看出要獲得MVP,個人數據包含得分、籃板、助攻、火鍋、抄截、Win Share的考量大於球隊戰績與年齡。這兩個主成分只能解釋55%的變異量,第3主成分仍有13%的變異量,所以我們可以用rgl套件中的plot3d()、text3d()、movie3d()繪製3D圖,來看看各球員在三維空間的位置。
> mvp<-cbind(mvp, pca_mvp$scores[,1:3]) #合併1~3主成分分數至原資料檔
> attach(mvp) #將mvp貼上搜尋路徑
> library(rgl) #載入rgl
> colors<-c("blue","red","darkgreen","purple","black") #指定顏色
> mvp[,2]<-as.factor(mvp[,2]) #將球員位置P的變數型態改為factor
> plot3d(x=Comp.1, y=Comp.2, z=Comp.3, col=colors, xlab="Component 1 with 30.5% Variance",
+ ylab="Component 2 with 24.4% Variance", zlab="Component 3 with 13.3% Variance") #繪製3D散布圖
> text3d(pca_mvp$scores[,1:3], texts=rownames(mvp), col=colors[factor(P)]) #加上球員名字
> play3d(spin3d(axis=c(1, 0, 0), rpm=3), duration=25) #製作3D動畫,以x軸為中心,轉速3,時間25
> play3d(spin3d(axis=c(0, 1, 0), rpm=3), duration=25) #製作3D動畫,以y軸為中心,轉速3,時間25
> play3d(spin3d(axis=c(0, 0, 1), rpm=3), duration=25) #製作3D動畫,以z軸為中心,轉速3,時間25
> movie3d(spin3d(axis=c(1, 0, 0), rpm=3), duration=25, movie="3d_pca_x", dir="c:/Users/USER/Downloads/") #輸出x軸3D動畫
> movie3d(spin3d(axis=c(0, 1, 0), rpm=3), duration=25, movie="3d_pca_y", dir="c:/Users/USER/Downloads/") #輸出y軸3D動畫
> movie3d(spin3d(axis=c(0, 0, 1), rpm=3), duration=25, movie="3d_pca_z", dir="c:/Users/USER/Downloads/") #輸出z軸3D動畫
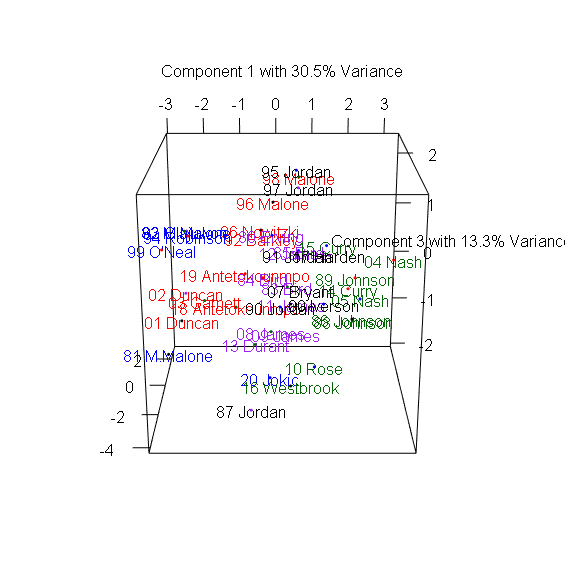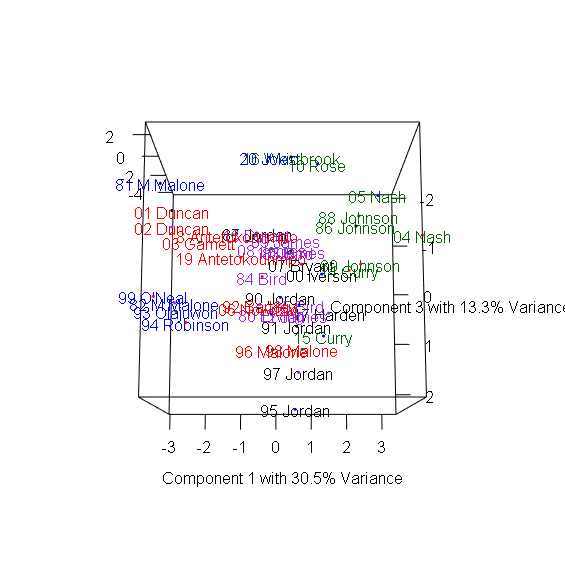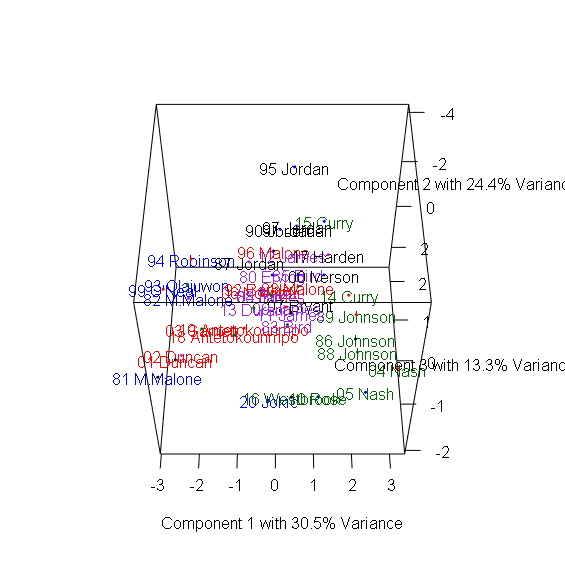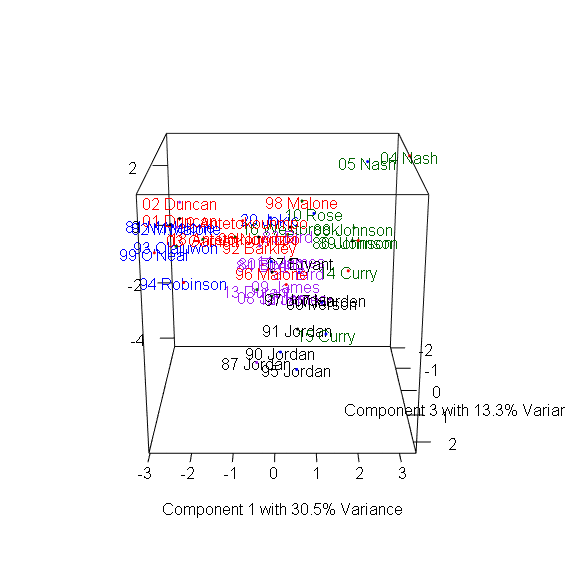

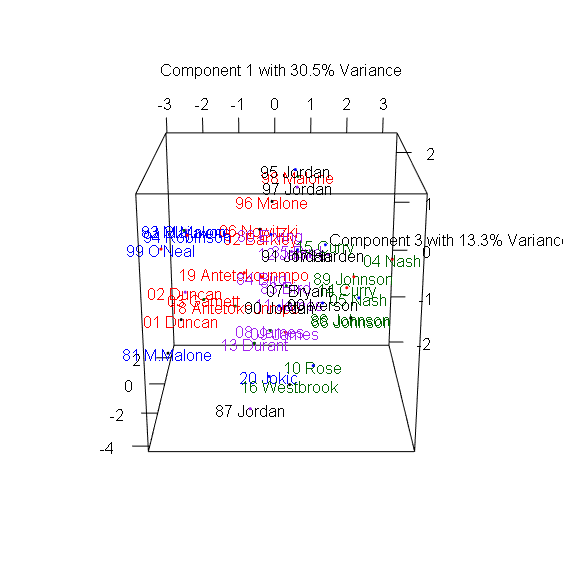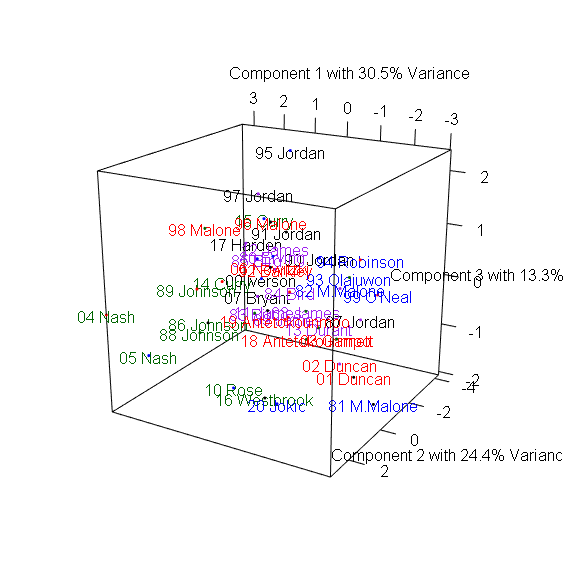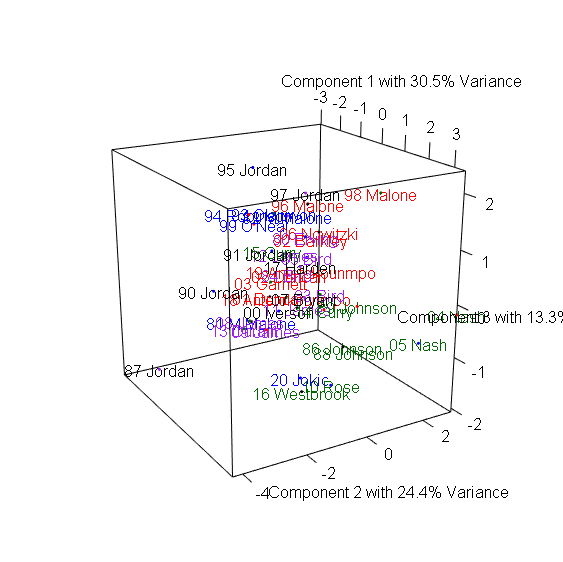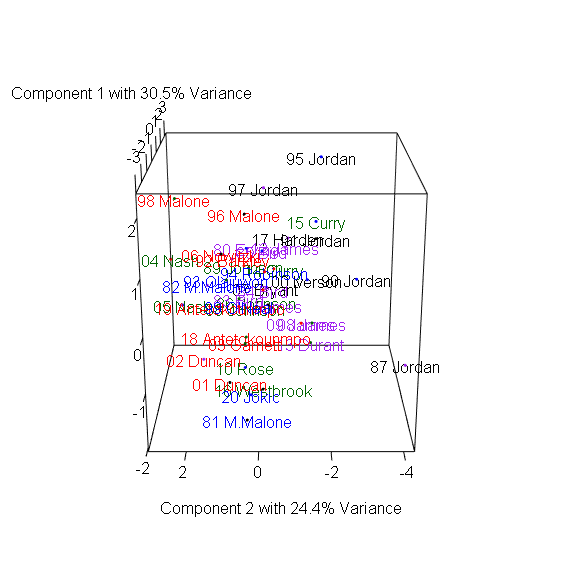
3D圖有趣之處在於多數球員都集中在中間,仍有幾個極端值顯示出這些球員在眾多MVP中出類拔萃,包含1981-1982年的Moses Malone、1987-1988年的MJ、1990-1991年的MJ、1995-1996的MJ、2004-2006的Steve Nash、2016-2017的Russel Westbrook。
Moses Malone在80年代初期以平均超過14個籃板,成為MVP中的籃板王。1986-1987正好是MJ拿下最有價值球員與最佳防守球員的球季,創下所有MVP中最高的Win Share,而1990-1991年的MJ則創下次高的Win Share,1995-1996 MJ締造了史無前例的72-10戰績。2004-2006兩季也正是Steve Nash帶領太陽一飛沖天的球季,他以超過30歲的年紀超越Magic Johnson,成為MVP中最老的助攻王。2016-2017的Russel Westbrook超越「大O障礙」,以平均30.8分、10.7籃板、10.5助攻,創下自Oscar Robertson 1961年以來再次有球員達到單季大三元的成就。