集群分析(cluster analysis)主要是辨別觀察值在某些特性上的相似處，並依照這些相似特性，將觀察值分類為不同集群。集群分析的目的在使同一群內具有高度同質性，不同群間有高度異質性。依方法不同集群分析可分為分割式(Partitional Clustering)與階層式(Hierarchical Clustering)，階層式不需要預設分群數目，可以透過電腦由上而下自動分群；分割式則需要先預設想要分群的數目，透過迭代讓群內差異變小，值到達到預設的分群數目為止。
與因素分析相較，集群分析是將觀察值劃分成不同集群，因素分析則是將同質性高的變數萃取成一群。集群分析把每個觀察值的變數視為m維空間，並計算m維空間點與點的距離；距離越近，觀察值同質性越高。如果兩個觀察值所有變數值都相同，兩點距離為0。一般而言以歐幾里得距離(Euclidean distance)、曼哈頓距離(Manhattan distance)測量m維空間的距離最為常見。
\[\text{Euclidean distance}(x,y)=\sqrt{(y_{1}-x_{1})^2+(y_{2}-x_{2})^2+...+(y_{n}-x_{n})^2}=\sqrt{\sum(y_{n}-x_{n})^2}\]
\[\text{Manhattan distance}(x,y)=|x_{1}-x_{2}|+|y_{1}-y_{2}|=\displaystyle\sum|x_{n}-y_{n}|\]
F1賽道分割式集群分析
分割式集群分析是在分群過程中將原有個案打散，並重新形成新的集群，k平均數法(k-means methods)是最常用的方法。k平均數法必須先決定分成k群，將資料依據歐幾里得距離分類到最近的集群中，直到所有資料分類完畢為止。
F1是世界最高等級的賽車比賽，每個賽季有10支車隊20位車手在16到25站的賽事中爭奪冠軍，這些大獎賽(Grand Prix)是封閉的專門賽道或是城市公路賽。英國車手Lewis Hamilton在2020年七度拿下世界冠軍，追平Michael Schumacher，同時又在2021年匈牙利完成101次桿位，在俄羅斯完成史無前例的生涯第100勝，是目前最成功的F1車手。
在眾多賽事中有幾條賽道為車迷所熟悉，包含摩納哥的街道賽、日本鈴鹿的8字型賽道、美國奧斯丁第一彎的雲霄飛車、義大利蒙札的高速殿堂、阿布達比的黃昏到黑夜。這些賽道特性影響著賽車調教甚至比賽結果。例如直線賽道需要大馬力、低風阻的懸吊；彎道多的賽道需要極大的下壓力來提升抓地力。
我們就以F1賽道作為分割式集群分析的例子，來看看這些賽道有什麼異同。賽道資料circuit.csv依序蒐集自F1.com、RACEFANS、Mercedes-AMG以及McLaren。首先先讀取資料：
> f1<-read.csv("c:/Users/USER/Downloads/circuit.csv", header=T, sep=",") #讀取賽道資料
> str(f1) #顯示資料結構
'data.frame': 22 obs. of 10 variables:
$ gpx : chr "Melbourne, Australia" "Bahrain, Bahrain" "Shanghai, China" "Baku, Azerbaijan" ...
$ circuit : chr "Albert Park Circuit" "Bahrain International Circuit" "Shanghai International Circuit" "Baku City Circuit" ...
$ laps : int 58 57 56 51 66 78 70 53 71 52 ...
$ length : num 5.3 5.41 5.45 6 4.67 ...
$ distance : num 308 308 305 306 308 ...
$ turn : int 16 15 16 20 16 19 14 15 10 18 ...
$ max.speed : num 321 330 348 337 322 ...
$ gear.change : int 46 56 51 78 48 47 52 58 32 40 ...
$ full.throttle : num 0.77 0.72 0.54 0 0.59 0.59 0.76 0.46 0.79 0.7 ...
$ elevation.change: num 2.6 16.9 7.4 26.8 29.6 42 5.2 33 63.5 11.3 ...
資料結構顯示檔案中共有22條賽道，包含賽道名稱、圈數、賽道長度、比賽距離、彎道數量、最高速度、換檔次數、全油門比例以及高低落差等資訊。由於比賽距離每條賽道都差不多因此忽略不計，我們將用剩下的資料來進行集群分析，得先將資料標準化，排除不同單位的影響。
> circuit<-data.frame(f1, row.names=f1$gpx) #將資料集的列改為賽道地點
> circuit<-subset(circuit, select=-c(gpx, circuit, distance)) #刪除賽道地點、賽道名稱、比賽距離
> circuit[1:3,] #顯示前三筆資料
laps length turn max.speed gear.change full.throttle elevation.change
Melbourne, Australia 58 5.303 16 321.0 46 0.77 2.6
Bahrain, Bahrain 57 5.412 15 329.6 56 0.72 16.9
Shanghai, China 56 5.451 16 348.0 51 0.54 7.4
> circuit<-scale(circuit) #資料標準化
決定最適分群數目
分割式集群分析最大的難題就是到底要將資料分為多少群？也就是最佳的分群數目為何？這個問題通常可以透過Elbow Method或Average Silhouette Method來尋求解決。
集群分析是使群內總變異最小，群間總變異最大，所以只要當資料被分成N群時，群內總變異(SSE)最小，N就會是最佳分群數，這個方法被稱為Elbow Method，就像手肘一樣，手肘開始彎曲的地方就是最佳分群數。而Average silhouette Method則計算Silhouette Coefficient來評估每個資料的內聚力和分散力，衡量分群效果。
這兩種方法我們可以用fviz_nbclust()，透過設定method="wss"或method="silhouette"參數來計算。
> library(factoextra) #載入factoextra
> fviz_nbclust(circuit, FUNcluster=kmeans, method="wss", k.max=10) #Elbow Method
> fviz_nbclust(circuit, FUNcluster=kmeans, method="silhouette", k.max=10) #Average Silhouette Method
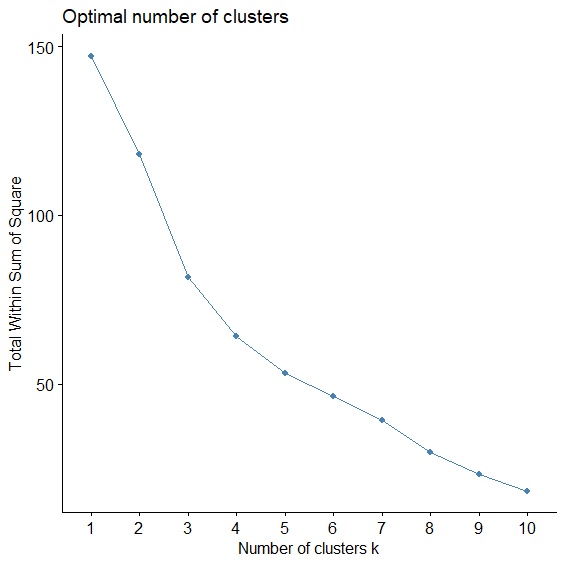
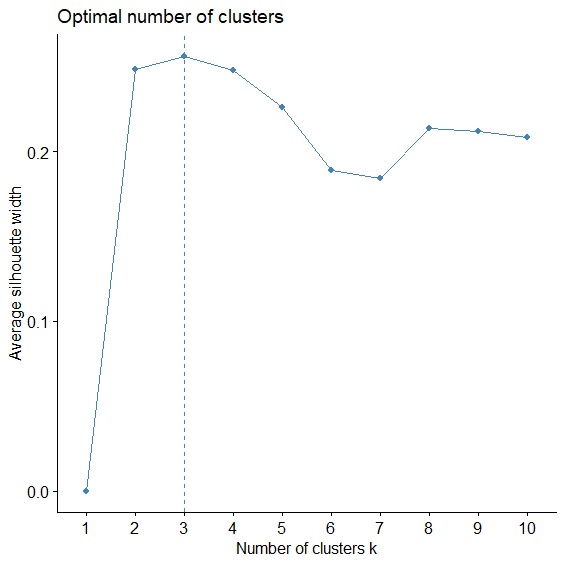
兩種判斷方法都顯示最佳分群數=3。
k平均數法
現在可以用kmeans()指令進行分割式集群分析，分群數依據剛才的結果設定為3群。
> cluster_kmeans<-kmeans(circuit, centers=3) #將資料分為3群
> cluster_kmeans #顯示分析結果
K-means clustering with 3 clusters of sizes 4, 8, 10
Cluster means:
laps length turn max.speed gear.change full.throttle elevation.change
1 -0.4225644 0.3445336 1.3965555 0.2390487 1.5688692 -0.91503272 -0.271782923
2 1.1646287 -1.0958421 -0.4630684 -0.6391014 -0.4475169 -0.01459484 0.131643378
3 -0.7626772 0.7388603 -0.1881675 0.4156617 -0.2695342 0.37768896 0.003398467
Clustering vector:
Melbourne, Australia Bahrain, Bahrain Shanghai, China
3 3 3
Baku, Azerbaijan Barcelona, Spain Monte Carlo, Monaco
1 2 2
Montreal, Canada Le Castellet, France Spielberg, Austria
2 3 2
Silverstone Circuit, UK Hockenheim, German Budapest, Hungary
3 2 2
Spa, Belgium Monza, Italy Singapore, Singapore
3 3 1
Sochi, Russia Suzuka, Japan Austin, USA
3 3 1
Mexico, Mexico Sao Paulo, Brazil Sepang, Malaysia
2 2 3
Abu Dhabi, UAE
1
Within cluster sum of squares by cluster:
[1] 13.62303 28.59076 39.38286
(between_SS / total_SS = 44.5 %)
Available components:
[1] "cluster" "centers" "totss" "withinss"
[5] "tot.withinss" "betweenss" "size" "iter"
[9] "ifault"
報表共分為四大部分，首先是集群分析的平均數，接下來是最重要的各賽道分群結果，第三部分是組內變異以及可解釋變異百分比，最後除了上述結果外kmean()可輸出的資訊還包含：
> cluster_kmeans$totss #totss 總平方和
[1] 147
> cluster_kmeans$withinss #withinss 組內變異
[1] 13.62303 28.59076 39.38286
> cluster_kmeans$tot.withinss #tot.withinss 組內總平方和
[1] 81.59665
> cluster_kmeans$betweenss #betweenss 組間變異
[1] 65.40335
> cluster_kmeans$size #size 每群的樣本數目
[1] 4 8 10
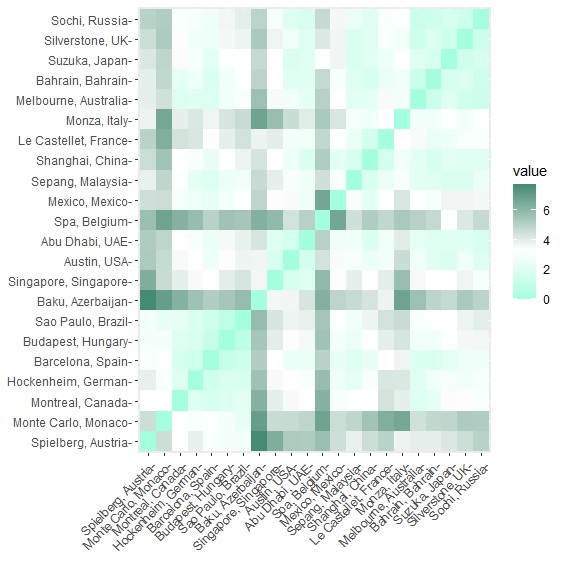
factoextra套件中的fviz_dist()以及fviz_cluster()可以視覺化呈現各賽道的歐幾里德距離，以及集群的分群結果：
> fviz_dist(get_dist(circuit, method="euclidean"), gradient=list(low = "aquamarine", mid = "white", high = "aquamarine4")) #視覺化各賽道歐幾里德距離
> fviz_cluster(cluster_kmeans, data=circuit, geom=c("text"), repel=TRUE) #視覺化集群分析結果
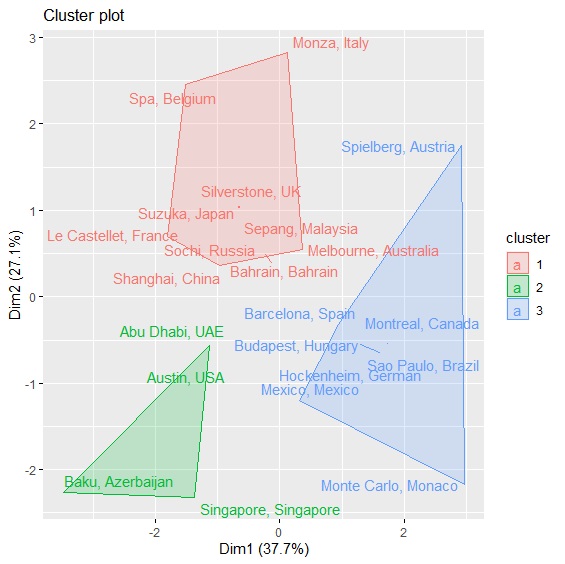
集群分析的最終結果將賽道分為3個群組，圖中左下方綠色賽道包含奧斯丁、阿布達比、巴庫等，屬於彎道多、換檔頻率高的賽道；藍色群組包含奧地利紅牛環、德國霍肯海姆、摩納哥蒙地卡羅等，則是屬於賽道長度短、比賽單圈多的賽道；最後紅色群組則多半屬於全油門頻率高的中高速賽道，包含義大利蒙札、比利時斯帕、英國銀石。最後可以將三個集群予以命名，並與原資料合併以利後續分析。
> type<-cluster_kmeans$cluster
> type<-factor(type, levels=c(1:3), labels=c("corner", "short circuit", "high-speed"))
> f1<-cbind(f1, type)
> table(f1$type)
corner short circuit high-speed
4 8 10
NBA50大球星階層式集群分析
階層式集群分析的優點是不需要事先決定要分幾群，可以讓電腦直接計算，事後再依據計算結果來將資料分群即可。
NBA在1996年選出50名球員，作為成立50週年的紀念，這50名球員也被稱為NBA 50大巨星。當年這份名單不考慮場上位置，完全由球員、教練、各隊經理及媒體票選。NBA50.csv整理出這50名球員的場均數據，我們用集群分析來替50大巨星分類。
> NBA50<-read.csv("c:/Users/USER/Downloads/NBA50.csv", header=T, sep=",")
> head(NBA50)
Player From To G MP PTS TRB AST STL BLK FG. X3P. FT. WS WS.48
1 Kareem Abdul-Jabbar 1970 1989 1560 36.8 24.6 11.2 3.6 0.9 2.6 0.559 0.056 0.721 273.4 0.228
2 Tiny Archibald 1971 1984 876 35.6 18.8 2.3 7.4 1.1 0.1 0.467 0.224 0.810 83.4 0.128
3 Paul Arizin 1951 1962 713 38.4 22.8 8.6 2.3 NA NA 0.421 NA 0.810 108.8 0.183
5 Rick Barry 1966 1980 794 36.3 23.2 6.5 5.1 2.0 0.5 0.449 0.330 0.735 177.2 0.216
6 Elgin Baylor 1959 1972 846 40.0 27.4 13.5 4.3 NA NA 0.431 NA 0.900 93.4 0.156
歐幾里德距離
NBA50.csv的資料包含每位球員的平均得分、籃板、助攻、抄截、火鍋、命中率、Win Share等等。由於早期NBA沒有將抄截、火鍋、三分球等納入統計，所以我們只將50位球員都有的得分、籃板、助攻、Win Share納入分析。
> main<-NBA50[,c("PTS", "TRB", "AST", "WS")] #選取得分、籃板、助攻、WS
> mean<-apply(main, 2, mean) #計算欄平均數，2代表column，1代表row
> sd<-apply(main, 2, sd) #計算欄標準差，2代表column，1代表row
> zscore<-scale(main, center=mean, scale=sd) #計算Z分數
> euclidean<-dist(zscore, method="euclidean") #用標準化z分數計算歐幾里得距離
計算完距離後，主要有五種方法可以依據距離遠近把資料分群：
- 最近距離法(single linkage method)：比較資料距離哪一個群體最近點的距離最近。公式為\(d(x,y)=\displaystyle\min_{i \in x, j \in y}(d_{ij})\)
- 最遠距離法(complete linkage method)：比較資料距離哪一個群體最遠點的距離最近。公式為\(d(x,y)=\displaystyle\max_{i \in x, j \in y}(d_{ij})\)
- 平均距離法(average method)：比較資料平均距離哪一個群體的距離最近。公式為\(d(x,y)=\frac{1}{N_{x}N_{y}}\sum_{i \in x}\sum_{j \in y} d_{ij}\)
- 中心法(centroid method)：比較資料距離哪一個群體中心點的距離最近。公式為\(d(x,y)=(|x-y|)^2\)
- 華德最小變異法(Ward's method)：Joe H. Ward Jr.在1963的論文Hierarchical Grouping to Optimize an Objective Function所提出。基本思想是同一群觀察值的變異數總和應該最小，不同群觀察值的變異數總和應該最大。透過比較組內總變異數大小，對組內總變異數增加最小的資料優先合併。
我們以華德最小變異法為例，對50大球星予以分群：
> cluster_eu<-hclust(euclidean, method="ward.D") #以Ward法進行集群分析
> plot(cluster_eu, labels=NBA50$Player, main="NBA 50 Greatest Players", xlab="Euclidean Distance") #繪製集群分析樹狀圖
> rect.hclust(cluster_eu, k=5, border="red") #以紅框標出5個集群
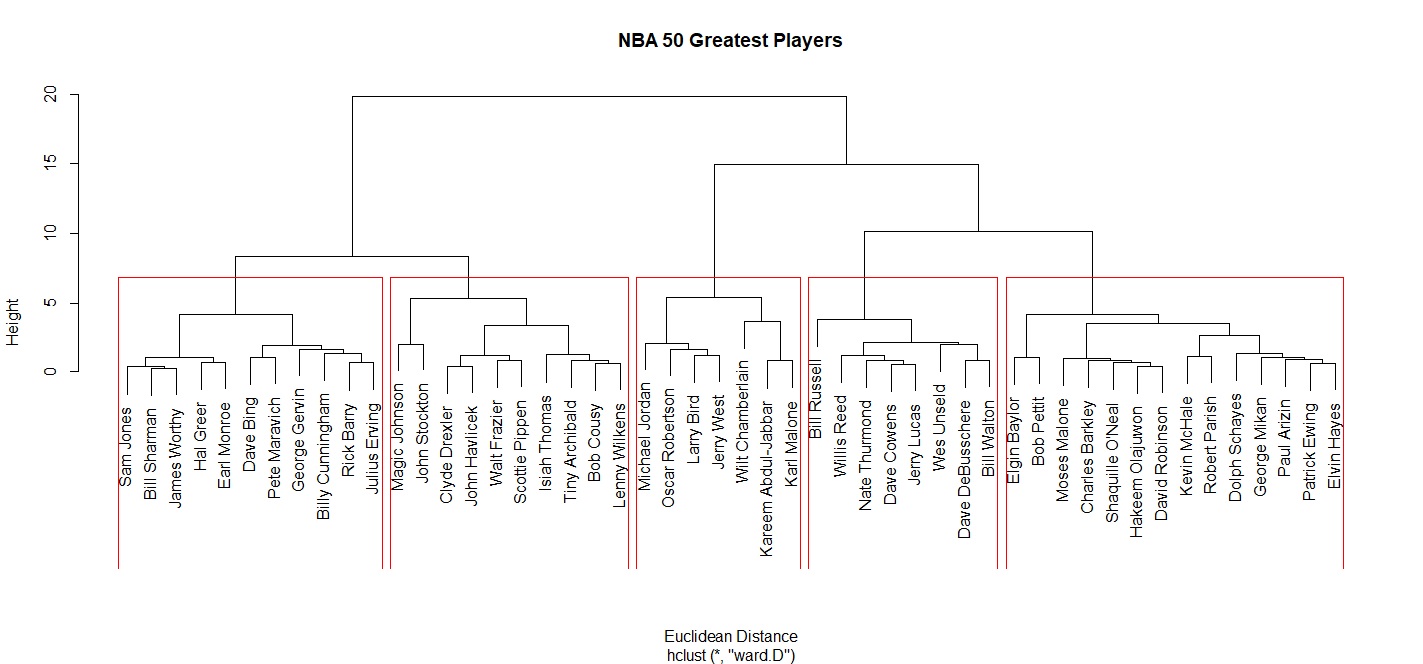
由上圖可以觀察到大體上可將NBA 50大巨星分為五個群體。由左至右包含了鋒線型的球員，例如James Worthy、Julius Erving。第二群則是偏控場傳球型的球員，例如Magic Johnson、John Stockton，有趣的是Clyde Drexler、Scottie Pippen也被分類在這一群。第三群則包含Michael Jordan、Wilt Chamberlain等得分高、Wing Share多的球員。 第四群則是籃板多的球員，包含Bill Russell、Bill Walton。最後一類則是包含四大中鋒等禁區球員。我們可以用cutree()呈現分群結果。
> Type<-cutree(cluster_eu, k=5)
> sapply(unique(Type), function(i)NBA50$Player[Type==i])
[[1]]
[1] "Kareem Abdul-Jabbar" "Larry Bird" "Wilt Chamberlain"
[4] "Michael Jordan" "Karl Malone" "Oscar Robertson"
[7] "Jerry West"
[[2]]
[1] "Tiny Archibald" "Bob Cousy" "Clyde Drexler" "Walt Frazier"
[5] "John Havlicek" "Magic Johnson" "Scottie Pippen" "John Stockton"
[9] "Isiah Thomas" "Lenny Wilkens"
[[3]]
[1] "Paul Arizin" "Charles Barkley" "Elgin Baylor"
[4] "Patrick Ewing" "Elvin Hayes" "Moses Malone"
[7] "Kevin McHale" "George Mikan" "Shaquille O'Neal
[10] "Hakeem Olajuwon" "Robert Parish" "Bob Pettit"
[13] "David Robinson" "Dolph Schayes"
[[4]]
[1] "Rick Barry" "Dave Bing" "Billy Cunningham"
[4] "Julius Erving" "George Gervin" "Hal Greer"
[7] "Sam Jones" "Pete Maravich" "Earl Monroe"
[10] "Bill Sharman" "James Worthy"
[[5]]
[1] "Dave Cowens" "Dave DeBusschere" "Jerry Lucas"
[4] "Willis Reed" "Bill Russell" "Nate Thurmond"
[7] "Wes Unseld" "Bill Walton"
或者也可以一個一個呼叫分群結果：
> NBA50$Player[Type==1]
[[1]]
[1] "Kareem Abdul-Jabbar" "Larry Bird" "Wilt Chamberlain"
[4] "Michael Jordan" "Karl Malone" "Oscar Robertson"
[7] "Jerry West"
集群分析的目的在於根據資料的相似度，來達到壓縮資料，降低雜訊的效果，利於後續分析。以50大球星為例，原本有多達50名球員，但經過集群後可以將50名球員歸類為五種類型。後續我們可將集群分類的結果與原資料合併，並賦予王牌球員(Ace)、場上指揮官(Floor Coach)、低位進攻者(Low-Post Master)、前鋒(Forward)、籃板專家(Rebound Leader)的分類名稱以利後續分析。
> Type<-factor(Type, levels=c(1:5), labels=c("Ace", "Floor Coach", "Low-Post Master", "Forward", "Rebound Leader"))
> NBA50_new<-cbind(NBA50, Type)
> head(NBA50_new)
Player From To G MP PTS TRB AST STL BLK FG. X3P. FT. WS WS.48 Type
1 Kareem Abdul-Jabbar 1970 1989 1560 36.8 24.6 11.2 3.6 0.9 2.6 0.559 0.056 0.721 273.4 0.228 Ace
2 Tiny Archibald 1971 1984 876 35.6 18.8 2.3 7.4 1.1 0.1 0.467 0.224 0.810 83.4 0.128 Floor Coach
3 Paul Arizin 1951 1962 713 38.4 22.8 8.6 2.3 NA NA 0.421 NA 0.810 108.8 0.183 Low-Post Master
4 Charles Barkley 1985 2000 1073 36.7 22.1 11.7 3.9 1.5 0.8 0.541 0.266 0.735 177.2 0.216 Low-Post Master
5 Rick Barry 1966 1980 794 36.3 23.2 6.5 5.1 2.0 0.5 0.449 0.330 0.900 93.4 0.156 Forward
檢驗集群分析
集群分析的目的是透過統計方法，讓每一群內的同質性高，群間的異質性大，所以我們可以透過變異數分析來檢驗集群分析的結果。
> anova(lm(NBA50_new$PTS~factor(Type)))
> anova(lm(NBA50_new$TRB~factor(Type)))
> anova(lm(NBA50_new$AST~factor(Type)))
> anova(lm(NBA50_new$WS~factor(Type)))
Royota Suzuki所撰寫的pvclust套件中pvclust()可以計算兩種不同的P值：au(Approximately Unbiased)及bp((Bootstrap Probability)。au是透過多層拔靴法(multiscale bootstrap resampling)來計算，一般情況會比以簡單拔靴法(normal bootstrap resampling)為基礎的bp來得精確。
無論是au或bp，都是評估階層式分群的是否達到顯著的參考。au或bp的數值介於0%到100%之間，數值越大表示分群的結果在數學上獲得強烈的支持。
> library(pvclust) #載入pvclust套件
> pvalue<-pvclust(t(zscore), method.hclust="ward.D", method.dist="euclidean", nboot=1000) ##pvclust以欄為分類基礎，因此先用t()進行行列轉置
Bootstrap (r = 0.5)... Done.
Bootstrap (r = 0.75)... Done.
Bootstrap (r = 1.0)... Done.
Bootstrap (r = 1.25)... Done.
> plot(pvalue, labels=NBA50$Player, main="NBA 50 Greatest Players with AU/BP Value(%)") #繪圖
> pvrect(pvalue, alpha=0.95) #以紅框標示出高度顯著的分群
曼哈頓距離
上述分析我們也可以改用曼哈頓距離來計算。可以看到相對於歐幾里德距離分為五群，曼哈頓距離只分為四個集群。
> manhattan<-dist(zscore, method="manhattan")
> cluster_man<-hclust(manhattan, method="ward.D")
> plot(cluster_man, labels=NBA50$Player, main="NBA 50 Greatest Players", xlab="Manhattan Distance")
> rect.hclust(cluster_man, k=4, border="red")
